|
Size: 504
Comment:
|
Size: 2972
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 17: | Line 17: |
| [[/ExampleCode]] | The PDF of an image can be calculated and displayed using the {{{pylab.hist}}} function or it can be calculated using the {{{scipy.histogram}}} function. === ASAR image of sea ice === {{attachment:seaice_intensity.png}} {{attachment:seaice_intensity_db.png}} The received power (intensity) of a radar system is proportional to the (normalized) radar backscatter coefficient {{{#!latex $\sigma^0(f,\theta)$ }}} as a function of frequency and incidence angle. The backscatter coefficient describes how much of the transmitted energy is backscattered from the surface media. A (calibrated) ASAR image ''img(y,x)=I'' is made of the measured intensities ''I'' which can be directly related to the backscatter coefficient. A value of zero means that no energy is reflected from the surface whereas a value of one means the total reflection. A useful representation of the intensity is the logarithmic transformation to the [[http://en.wikipedia.org/wiki/Decibel| decibel unit]] {{{#!python img_dB=10*log10(img) }}} The PDF of the image above can be estimated from the number of occurrence of grey levels in the ''B'' intervals between ''q'' and ''q+dq'' and displayed using {{{#!python hist(img,bins=50) }}} with the resolution ''B'' for 50 ''bins'' (intervals). {{attachment:seaice_histogram.png}} [[/ExampleCode|Source code and data]] == Estimation of the PDF parameters == {{attachment:model_stat.png}} {{{#!python from scipy import * from pylab import * import scipy.optimize as opti import scipy.stats as stats def my_pdf(p,x): """A linear mixture of two gamma functions""" pdf1=stats.gamma.pdf(x,p[0],loc=p[1],scale=p[2]) pdf1/=sum(pdf1) pdf2=stats.gamma.pdf(x,p[3],loc=p[4],scale=p[5]) pdf2/=sum(pdf2) pdf=pdf1*p[6]+pdf2*p[7] return pdf def my_cost(p,x,y): """The cost (error) function""" f=my_pdf(p,x) return y-f img=reshape(fromfile('ASAR_seaice_mixed_20080421_f32_1000x1000.dat',dtype=float32),(1000,1000)) close('all') h=histogram(img,bins=500) y,x=h[0].astype(float64)/sum(h[0]),h[1].astype(float64) plot(x,y) p0=[7.0,0.003,0.005,7.0,0.1,0.005,0.5,0.5 ] # initial guess p,success = opti.leastsq(my_cost, p0[:], args = (x, y)) y_fit=my_pdf(p,x) plot(x,y_fit) axis([0,0.3,0,0.023]) legend(('Observed PDF','Optimized model PDF'),'upper right') xlabel('Backscatter coefficient') ylabel('Probability') savefig('model_stat.png',dpi=100) show() }}} |
Random variables
The measurements that form an image show statistical fluctuations. The image is characterised by a probability density function (PDF). The PDF f describes the probability of the occurrence of a discrete grey level q in the range of grey levels Q.
latex error! exitcode was 2 (signal 0), transscript follows:
Probability density functions and histograms
The PDF of an image can be calculated and displayed using the pylab.hist function or it can be calculated using the scipy.histogram function.
ASAR image of sea ice
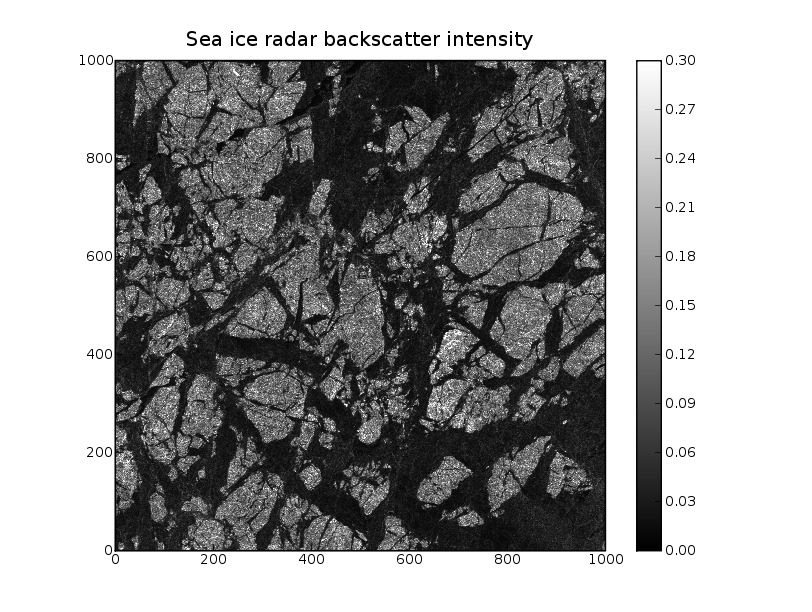
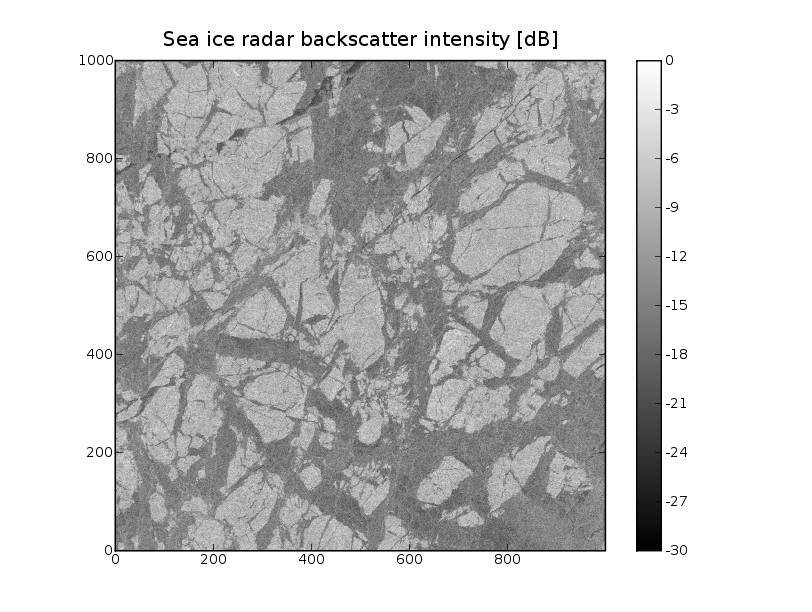
The received power (intensity) of a radar system is proportional to the (normalized) radar backscatter coefficient
latex error! exitcode was 2 (signal 0), transscript follows:
as a function of frequency and incidence angle. The backscatter coefficient describes how much of the transmitted energy is backscattered from the surface media.
A (calibrated) ASAR image img(y,x)=I is made of the measured intensities I which can be directly related to the backscatter coefficient. A value of zero means that no energy is reflected from the surface whereas a value of one means the total reflection.
A useful representation of the intensity is the logarithmic transformation to the decibel unit
1 img_dB=10*log10(img)
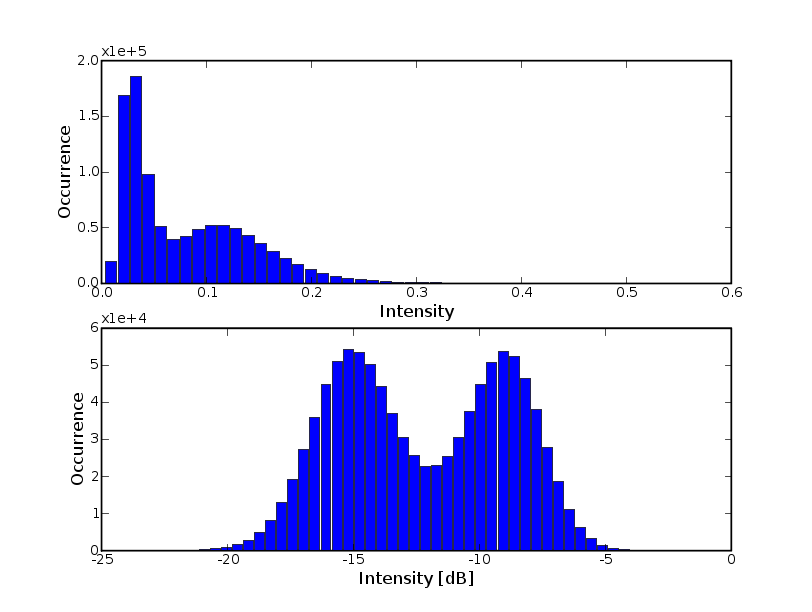
The PDF of the image above can be estimated from the number of occurrence of grey levels in the B intervals between q and q+dq and displayed using
1 hist(img,bins=50)
with the resolution B for 50 bins (intervals).
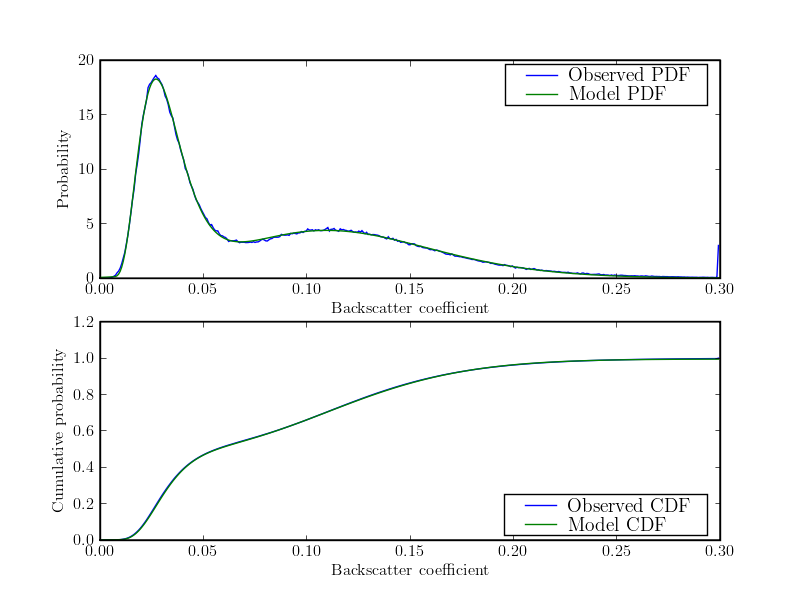
Estimation of the PDF parameters
1 from scipy import *
2 from pylab import *
3 import scipy.optimize as opti
4 import scipy.stats as stats
5
6
7 def my_pdf(p,x):
8 """A linear mixture of two gamma functions"""
9 pdf1=stats.gamma.pdf(x,p[0],loc=p[1],scale=p[2])
10 pdf1/=sum(pdf1)
11 pdf2=stats.gamma.pdf(x,p[3],loc=p[4],scale=p[5])
12 pdf2/=sum(pdf2)
13 pdf=pdf1*p[6]+pdf2*p[7]
14 return pdf
15
16 def my_cost(p,x,y):
17 """The cost (error) function"""
18 f=my_pdf(p,x)
19 return y-f
20
21 img=reshape(fromfile('ASAR_seaice_mixed_20080421_f32_1000x1000.dat',dtype=float32),(1000,1000))
22
23 close('all')
24 h=histogram(img,bins=500)
25 y,x=h[0].astype(float64)/sum(h[0]),h[1].astype(float64)
26
27
28 plot(x,y)
29 p0=[7.0,0.003,0.005,7.0,0.1,0.005,0.5,0.5 ] # initial guess
30
31 p,success = opti.leastsq(my_cost, p0[:], args = (x, y))
32 y_fit=my_pdf(p,x)
33 plot(x,y_fit)
34 axis([0,0.3,0,0.023])
35 legend(('Observed PDF','Optimized model PDF'),'upper right')
36 xlabel('Backscatter coefficient')
37 ylabel('Probability')
38 savefig('model_stat.png',dpi=100)
39 show()
