Arbeitsgruppe 2 : Nina Maaß, Bente Tiedje
Ziel/Aufgabe: Die heruntergeladenen Satellitendaten sollen so bearbeitet werden, dass sie mit der ECOHAM-Modellgitterstruktur (88x82 Boxen) übereinstimmen. Anschließend sollen sie auf das Modellgebiet (Nordseeregion) verkleinert werden.
Einfaches Einlesen, Ausschneiden und Darstellen
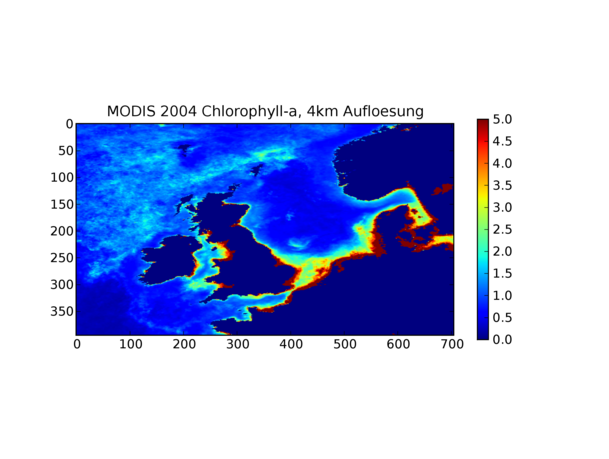
Mit diesem Programm werden die Daten (A20040012004366.L3m_YR_CHLO_4) eingelesen. Durch einfache Umrechnung der Zeilen und Spalten der "Datenmatrix" in Breiten- und Längengrade werden die am nächsten liegenden geographischen Eckpunkte des ECOHAM-Modellgebiet ermittelt. Anschließend wird das ECOHAM-Modellgebiet ausgeschnitten und dargestellt (siehe Abbildung 1). Da Rundungen vorgenommen werden müssen, wird nicht das exakte Modellgebiet ausgeschnitten. Eine weitaus genauere Berechnung des Modellgebietes liefert erst das nachfolgende Programm.
1 from scipy import *
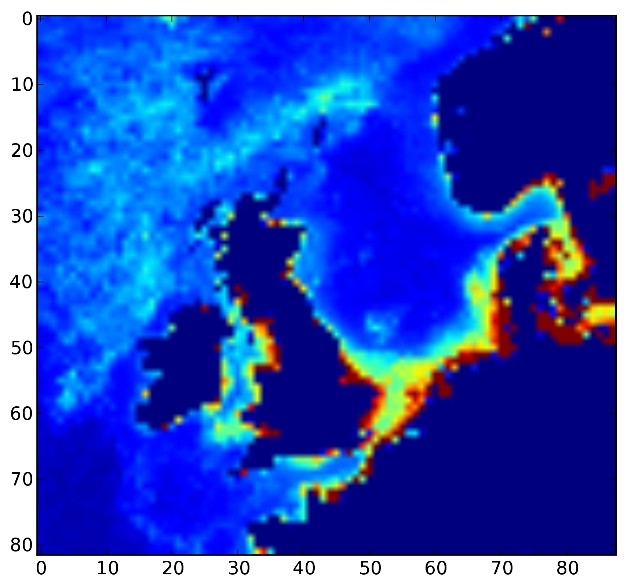
2 Abbildung 4
3 import gdal
4 import struct
5 from pylab import *
6
7 filename='/pf/u/u243066/satdat/chlorophyll/A20040012004366.L3m_YR_CHLO_4'
8 f=gdal.Open(filename)
9 metadata=f.GetMetadata()
10 a=f.GetRasterBand(1)
11 scanline = a.ReadRaster( 0, 0, a.XSize, 1, a.XSize, 1, gdal.GDT_Float32 )
12
13 img=zeros((a.YSize,a.XSize),float)
14 for yi in range(a.YSize-1):
15 scanline=struct.unpack("f"*a.XSize,a.ReadRaster(0,yi,a.XSize,1,a.XSize,1,gdal.GDT_Float32))
16 img[yi,:]=((array(scanline).astype(float)).astype(float))
17
18 #img enthält Daten für gesamte Erde:90°N-90°S, 180°W-180°O
19
20 #damit die Landfläche dunkelblau erscheint, also in der "Farbe" von Null
21 img[(img==65535).nonzero()]=0
22
23 ##ECOHAM3/4-Gebiet ausschneiden
24 ##ECOHAM3/4 Latitude:47.5833 to 63.9833, Longitude:-15.25 to 14.0833
25
26 ecolat1=63.9833
27 ecolat2=47.5833
28 ecolon1=-15.25
29 ecolon2=14.0833
30 latstep=float(metadata['Latitude Step'])
31 lonstep=float(metadata['Longitude Step'])
32 Nlat=float(metadata['Northernmost Latitude'])
33 Wlon=float(metadata['Westernmost Longitude'])
34
35 lat1=floor((Nlat-ecolat1)/latstep)#obere Breitengradbegrenzung des Gebietes
36 lat2=ceil((Nlat-ecolat2)/latstep) #untere Breitengradbegrenzung des Gebietes
37 lon1=floor((abs(Wlon-ecolon1))/lonstep)#linke Längengradbegrenzung des Gebietes
38 lon2=ceil((abs(Wlon-ecolon2))/lonstep)#rechte Längengradbegrenzung des Gebietes
39
40 #Ausschneiden des Gebietes
41 img_eco34=img[lat1:lat2,lon1:lon2]
42
43 #Skalierung der Daten (siehe key 'Scaling Equation' in metadata):
44 img_eco34_chlo=float(metadata['Base'])**((float(metadata['Slope'])*img_eco34)
45 +float(metadata['Intercept']))
46 #Plotten
47 figure(1)
48 imshow(img_eco34_chlo,vmin=0,vmax=5)
49 title('MODIS 2004 Chlorophyll 4km')
50 colorbar(shrink=0.6)
51 show()
Abbildung 1: Ergebnis-Plot des Programmcodes
Anpassen an Modellgitterstruktur (und Ausschneiden)
Um den nachfolgenden Programmcode besser nachvollziehen zu können, wird er jetzt kurz erklärt. Die Abbildungen 2 und 3 veranschaulichen verwendete Konstantenbezeichnungen.
- Zunächst wird das Modellgitter (Gitterweite N-S: 0,2° und O-W: 0,333°) auf die ganze Erde ausgeweitet. Anschließend wird berechnet wie groß die Differenzen zwischen den Ausmaßen der Satellitendaten (90°N bis 90°S, 180°W bis 180°O) und den Ausmaßen des erweiterten Modellgebietes sind. Das Verhältnis der Differenzen vom linken zum rechten Rand beträgt 1:3 (vergleiche Ofaktor) und vom oberen zum unteren Rand 1:11 (vergleiche Sfaktor).
- Die Satellitendaten werden nun mit Hilfe der zoom-Funktion so unterteilt (interpoliert), dass eine Schrittweite in N-S-Richtung der berechneteten Differenz des oberen Randes und eine Schrittweite in O-W-Richtung der berechneten Differenz des linken Randes entspricht (siehe Zeile 66).
- Von den Satellitendaten werden die erste Zeile und erste Spalte, sowie die 11 letzten Zeilen und die 3 letzten Spalten "abgeschnitten" (Zeile 72).
- Auf diese übrig gebliebenen Daten (img_cut1) wird die zoom-Funktion so angewandt, dass die Schrittweiten den Gitterweiten des Modells entsprechen.
- Die Eckpunkte des Modellgebietes (lat1, lat2, lon1, lon2) werden berechnet und das Modellgebiet wird ausgeschnitten (Zeile 79 bis 84). Die ausgeschnittenen Daten (img_cut2) haben nun genausoviele Zeilen und Spalten wie das Modell Boxen in lateraler und longitudinaler Richtung hat, nämlich 82x88.
- img_cut2 wird als hdf-Datei gespeichert und zur Veranschaulichung graphisch dargestellt (siehe Abbildung 4).
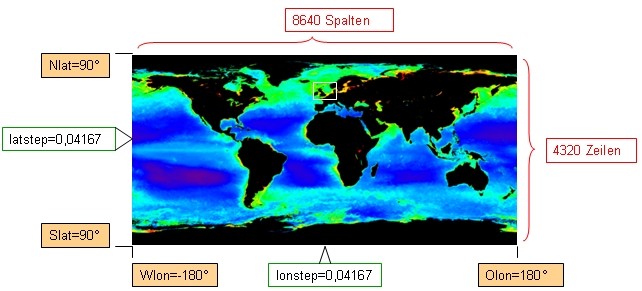 Abbildung 2
Abbildung 2
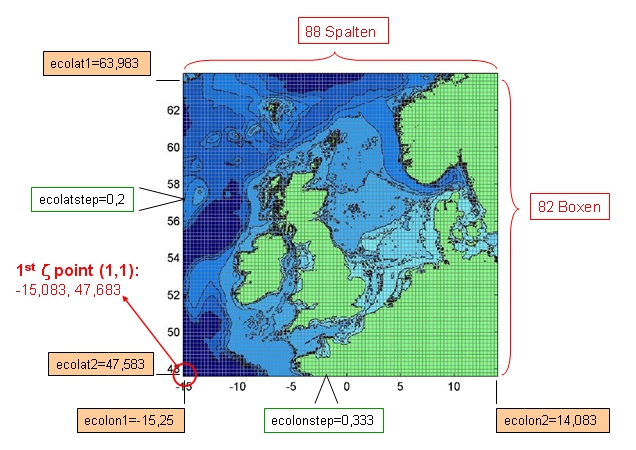 Abbildung 3
Abbildung 3
1 from scipy import *
2 import struct
3 from pyhdf.SD import *
4 from pylab import *
5
6 def read_CHLO(filename):
7 # Oeffne HDF4-Datei
8 f=SD(filename)
9 # Hole die Attribute (Metadata)
10 attr = f.attributes()
11 # Hole die in der Datei verfuegbaren Datensaetze
12 dsets = f.datasets()
13 # Hole die Daten aus der Datei in ein scipy.array
14 data=array(f.select('l3m_data').get())
15 # Siehe attr:
16 #'Scaling Equation': ('Base**((Slope*l3m_data) + Intercept) = Parameter value\x00',
17 Base=attr['Base']
18 Slope=attr['Slope']
19 Intercept=attr['Intercept']
20 data[(data==65535).nonzero()]=nan
21 # Skaliere die Daten, um die urspruenglichen Einheiten zu berechnen
22 data=Base**((Slope*data) + Intercept)
23 return data,attr
24
25 def hdf_set(filename,z):
26 hdfFile=filename
27 f = SD(hdfFile,SDC.WRITE|SDC.CREATE)
28 f.author = 'Lars Kaleschke'
29 v2=f.create('z',SDC.FLOAT32,(z.shape[0],z.shape[1]))
30 v2[:]=z.astype(float32)
31 f.end()
32 return
33
34 filename='/pf/u/u243066/satdat/chlorophyll/A20040012004366.L3m_YR_CHLO_4'
35 img,metadata=read_CHLO(filename)
36
37 ##ECOHAM3/4-Gebiet ausschneiden
38 ##ECOHAM3/4 Latitude:47.5833 to 63.9833, Longitude:-15.25 to 14.0833
39
40 ecolatstep=0.2
41 ecolonstep=1./3.
42 ecolat1=63.9833
43 ecolat2=47.5833
44 ecolon1=-15.25
45 ecolon2=14.0833
46 latstep=float(metadata['Latitude Step'])
47 lonstep=float(metadata['Longitude Step'])
48 Nlat=float(metadata['Northernmost Latitude'])
49 Wlon=float(metadata['Westernmost Longitude'])
50 Slat=float(metadata['Southernmost Latitude'])
51 Olon=float(metadata['Easternmost Longitude'])
52
53 #Anpassung des Satellitenbildrandes an Modellrand:
54 modrand_N=ecolat1+floor((Nlat-ecolat1)/ecolatstep)*ecolatstep
55 modrand_W=ecolon1+ceil((Wlon-ecolon1)/ecolonstep)*ecolonstep
56 modrand_S=ecolat1+ceil((Slat-ecolat1)/ecolatstep)*ecolatstep
57 modrand_O=ecolon1+floor((Olon-ecolon1)/ecolonstep)*ecolonstep
58
59 #Berechnung der neuen Unterteilung des Satbildgitters fuer optimales Abschneiden:
60
61 zoom11=abs(latstep/(Nlat-modrand_N)) #Berechnung des zoom-Faktors
62 zoom12=abs(lonstep/(Wlon-modrand_W))
63 Sfaktor=int(round(abs(Slat-modrand_S)/(Nlat-modrand_N)))
64 Ofaktor=int(round((Olon-modrand_O)/abs(Wlon-modrand_W)))
65
66 img_zoom1=ndimage.zoom(img,(zoom11,zoom12)) #Default-Einstellung für Grad der zoom-Funktion: order=3
67
68 #Abschneiden der ueberstehenden Pixel im Satbild:
69 s=img_zoom1.shape
70 s1=s[0]-Sfaktor-1
71 s2=s[1]-Ofaktor-1
72 img_cut1=img_zoom1[1:s1,1:s2]
73
74 #Anpassung des Satellitenbildes an Modellgitter:
75 zoom21=(180./s[0])/0.2
76 zoom22=(360./s[1])/(1./3.)
77 img_zoom2=ndimage.zoom(img_cut1,(zoom21,zoom22)) #Default-Einstellung für Grad der zoom-Funktion: order=3
78
79 #Ausschneiden des Modellausschnitts aus Satbild:
80 lat1=int(round((modrand_N-ecolat1)/ecolatstep))
81 lat2=int(round((modrand_N-ecolat2)/ecolatstep))
82 lon1=int(round(abs(modrand_W-ecolon1)/ecolonstep))
83 lon2=int(round(abs(modrand_W-ecolon2)/ecolonstep))
84 img_cut2=img_zoom2[lat1:lat2,lon1:lon2]
85
86 #Speichern von img_cut2 als hdf-Datei:
87 filename='Satimg_cut_Eco34.hdf'
88 hdf_set(filename,img_cut2)
89
90 #Plotten von img_cut2:
91 figure(3)
92 imshow(nan_to_num(img_cut2),vmin=0,vmax=5)
93 show()
Abbildung 4: Ergebnis-Plot des Programmcodes