Introduction
This model is to simulate the El Niño–Southern Oscillation effect.
Example in Python GUI
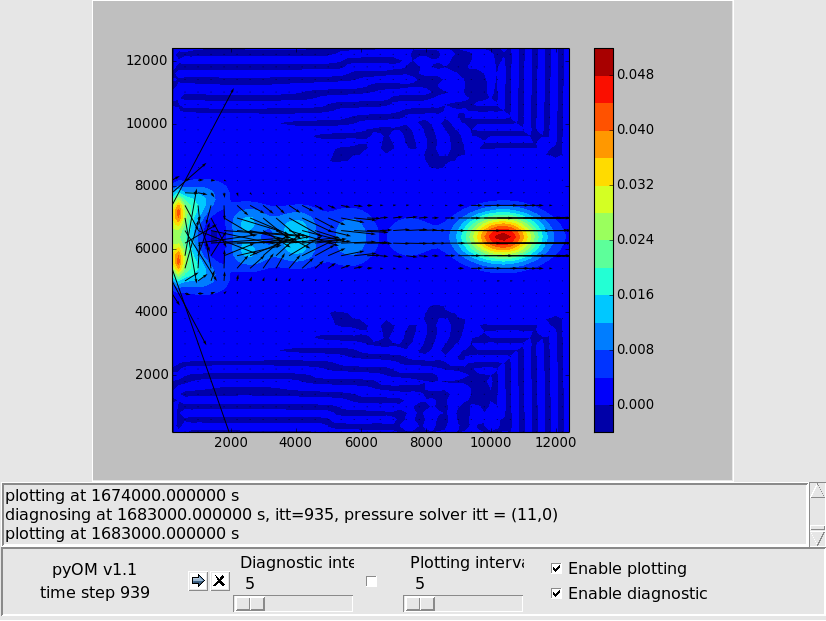
Reference
Olbers, Dirk, Willebrand, Jürgen, Eden, Carsten. Ocean Dynamics. Springer, 2012. Print
Source Code
1 import sys; sys.path.append('../py_src')
2 from pyOM_gui import pyOM_gui as pyOM
3 from numpy import *
4
5 BETA=2e-11
6
7 class enso1(pyOM):
8 """ Enso response
9 """
10 def set_parameter(self):
11 """set main parameter
12 """
13 M=self.fortran.pyom_module
14 M.nx = 64
15 M.nz = 3
16 M.ny = 64
17 M.dx = 200e3
18 M.dz = (500e3**2*BETA) **2 /9.81
19 M.dt = 3600.0 /2.
20 M.eps2d_sor = 1e-22
21 M.enable_hydrostatic = 1
22 M.enable_cyclic_x = 0
23 M.enable_quicker_advection = 1
24 M.enable_quicker_mom_advection= 1
25 M.enable_free_surface = 1
26 return
27
28 def set_coriolis(self):
29 """ vertical and horizontal Coriolis parameter on yt grid
30 routine is called after initialization of grid
31 """
32 M=self.fortran.pyom_module
33 f0=-M.ny*M.dx/2.0*BETA # equatorial beta plane
34 M.coriolis_t[:] = f0+BETA*M.yt[:]
35 M.coriolis_hor[:] = 0.
36 return
37
38 def initial_conditions(self):
39 """ setup all initial conditions
40 """
41 M=self.fortran.pyom_module
42 cn = (M.dz*9.81)**0.5
43 hn=cn**2/9.81
44 Re = (cn /BETA)**0.5
45 y0=M.ny*M.dx*0.5
46 g=9.81
47 A = .1
48 for i in range(M.nx):
49 for j in range(M.ny):
50 M.eta[i,j,:]=0.1*exp( -(M.xt[i]-y0*0.3)**2/(2*Re)**2 \
51 -(M.yt[j]-y0)**2/(2*Re)**2 )
52 return
53
54 def make_plot(self):
55 """ make a plot using methods of self.figure
56 """
57 if hasattr(self,'figure'):
58 M=self.fortran.pyom_module # fortran module with model variables
59 x=M.xt[1:-1]/1e3
60 y=M.yt[1:-1]/1e3
61
62 self.figure.clf()
63 ax=self.figure.add_subplot(111)
64 a=M.eta[1:-1,1:-1,M.tau-1]
65 co=ax.contourf(x,y,a.transpose(),15)
66 ax.axis('tight')
67
68 a=M.u[1:-1:2,1:-1:2,1,M.tau-1]
69 b=M.v[1:-1:2,1:-1:2,1,M.tau-1]
70 ax.quiver(x[::2],y[::2],a.transpose(),b.transpose() )
71 self.figure.colorbar(co)
72 return
73
74 if __name__ == "__main__": enso1(snapint = 5).mainloop()
