Zusammenfassung Konvektionszellen
Einleitung
Konvektion ist neben der Wärmeleitung und Wärmestrahlung, ein Mechanismus zur Wärmeübertragung von thermischer Energie von einem Ort zu einem anderen. Dieser ist mit einem Transport von Teilchen verbunden, die thermische Energie mit sich führen. Konvektion wird im Ozean und in der Atmosphäre meist durch Dichteänderungen - durch Abkühlung oder Erwärmung - hervorgerufen und beschreibt die vertikale, turbulente Bewegung von Wasser bzw. Luft. Rayleigh-Benard-Konvektion entsteht, wenn ein vollständig mit Wasser gefülltes Gefäß von unten erhitzt und von oben gekühlt wird. Warmes Wasser steigt auf, während kaltes nach unten sinkt. Die stabile Schichtung schlägt aufgrund der treibenden Temperaturdifferenz um und es entstehen komplexe Strukturen in Form von geometrisch strukturierten, vertikal angeordneten Konvektionszellen, die in der Draufsicht eine hexagonale Zellenstruktur annehmen.
Auch in der atmosphärischen Grenzschicht über dem Ozean können sich Konvektionszellen bilden, wenn kalte Luft vom Ozean erwärmt wird. Überlagert mit einem mitteleren Wind können sich auch Konvektionsrollen ergeben, deren Achsenorientierung zwischen mittlerer Windrichtung an der Oberfläche und geostrophischem Wind über der Grenzschicht verläuft. Die Dicke der Grenzschicht, in der eine Inversion auftritt und die Mächtigkeit der Konvektionsrolle stimmen dabei gewöhnlich überein. Das Verhältnis des Zellen-Durchmessers zu Schichtdicke beträgt laut Rayleigh-Bènard-Theorie 2.8, Beobachtungen zeigen am häufigsten einen Wert von etwa 3.
Um in der Natur vorkommenden Konvektionszellen zu untersuchen, wurden Satellitenbilder ausgewertet. Kaltluftausbrüche über der Framstraße verursachen eine Erwärmung der Atmosphäre über dem Ozean. Diese Heizung von unten führt zu Konvektionszellen, die man anhand der Wolkenbilder erkennen und räumlich bemessen kann. Reanalyse-Daten der Temperatur in der Atmosphäre werden dann genutzt, um die Dicke der Grenzschicht abzuschätzen und das theoretisch hergeleitete Verhältnis des Durchmessers zur Mächtigkeit zu überprüfen. Zur Analyse wurde ein Bild vom 13.03.2009 aufgenommen vom MODIS Aqua Sensor verwendet
Code zur Kartendarstellung
1 import Image
2 from pylab import *
3 from mpl_toolkits.basemap import Basemap
4 import numpy as np
5
6 def load_img(filename):
7 im=Image.open(filename)
8 return resize(fromstring(im.tostring(),uint8),(im.size[1],im.size[0],3))
9
10 import scipy.ndimage as nd
11 # define coordinates of profile
12 lat_glatt=[77.0,78.0,79.0]
13 lon_glatt_start,lon_glatt_stop=2.0,10.0
14
15
16
17 filename='AERONET_Hornsund.2009072.aqua.250m.jpg'
18
19
20 a=load_img(filename)
21
22 a=nd.zoom(a[:,:,0],0.2)
23
24 north=80.2363
25 south=73.7612
26 east=40.4156
27 west=-9.3026
28
29 filename='AERONET_Hornsund.2009072.aqua.250m.jgw'
30 cds=array(open(filename).read().split('\n')[:-1]).astype(float)
31
32
33
34 [yn,xn]=shape(a)
35
36 # make grid
37 x=linspace(west,east,xn)
38 y=linspace(north,south,yn)
39
40 [lons,lats] = meshgrid(x,y)
41
42 start=find(x>lon_glatt_start)[0]
43 stop=find(x>lon_glatt_stop)[0]
44
45 line=[]
46 for i in lat_glatt:
47 line.append(find(y<i)[0])
48
49 figure(2)
50
51 m=Basemap(projection='merc',llcrnrlat=74,urcrnrlat=80,llcrnrlon=-9,urcrnrlon=20,resolution='h')
52
53 xm,ym=m(lons,lats)
54
55 xi=linspace(m.llcrnrx,m.urcrnrx,xn) # define the new grid
56 yi=linspace(m.llcrnry,m.urcrnry,yn)
57 modis_img_nmpg=griddata(xm.flatten(),ym.flatten(),a.flatten(),xi,yi)
58
59
60 m.imshow(modis_img_nmpg,cm.bone, interpolation='bilinear',aspect='auto')
61 m.drawcoastlines()
62 m.fillcontinents(color='gray',lake_color='aqua')
63 m.drawmapboundary(fill_color='aqua')
64
65 m.drawmeridians(np.arange(0,360,5),labels=[1,0,0,1])
66 m.drawparallels(np.arange(-90,90,2),labels=[0,1,0,1])
67
68 cls=('ryg')
69 for k,i in enumerate(line):
70 x1,y1=m(x[start],y[i])
71 x2,y2=m(x[stop],y[i])
72 m.plot([x1,x2],[y1,y2],'-'+cls[k],linewidth=3)
73
74
75
76 for j in range(182,191):
77 x,y=m(j-180.,77)
78 m.plot(x,y,'b.',markersize=12)
79 x,y=m(j-180.,78)
80 m.plot(x,y,'b.',markersize=12)
81 x,y=m(j-180.,79)
82 m.plot(x,y,'b.',markersize=12)
83
84 show()
85 savefig('modis_test.png')
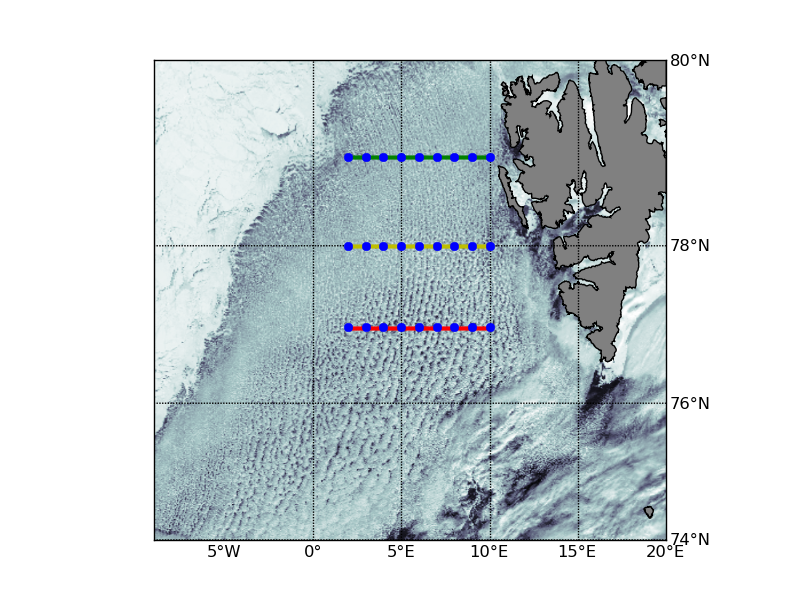
Längenspektren über die Profile
1 import Image
2 from pylab import *
3 from mpl_toolkits.basemap import Basemap
4 import numpy as np
5 from scipy import ndimage
6
7 def load_img(filename):
8 im=Image.open(filename)
9 return resize(fromstring(im.tostring(),uint8),(im.size[1],im.size[0],3))
10
11 def mitteln(bild,ref_y,ref_x_start,ref_x_stop,h):
12 y_inds=range(ref_y-h,ref_y+h)
13 tempo=zeros([len(y_inds),ref_x_stop-ref_x_start])
14 k=0
15 for i in y_inds:
16 tempo[k,:]=a[i,ref_x_start:ref_x_stop,0]
17 k=k+1
18
19 out=mean(tempo,0)
20 return out
21
22 # define coordinates of profile
23 lat_glatt=79.0
24 lon_glatt_start,lon_glatt_stop=2.0,10.0
25
26
27 # load data
28 filename='AERONET_Hornsund.2009072.aqua.250m.jpg'
29
30 a=load_img(filename)
31
32
33 north=80.2363
34 south=73.7612
35 east=40.4156
36 west=-9.3026
37
38 [yn,xn,dum]=shape(a)
39
40 # make grid
41 x=linspace(west,east,xn)
42 y=linspace(north,south,yn)
43
44 [lons,lats] = meshgrid(x,y)
45
46 start=find(x>lon_glatt_start)[0]
47 stop=find(x>lon_glatt_stop)[0]
48 line=find(y<lat_glatt)[0]
49
50 test=mitteln(a,line,start,stop,30)
51 test=ndimage.gaussian_filter1d(test,3)
52
53 # power spectrum
54 figure(1)
55 [pxx,freq]=psd(test,NFFT=512,Fs=1,Fc=0,detrend=mlab.detrend_linear,window=mlab.window_hanning, noverlap=0)
56
57 # plot spectrum selber
58 figure(2)
59 freq=0.25/freq
60 plot(freq[1:],pxx[1:],'g-')
61 xlim((0,40))
62 xlabel('Zelldurchmesser [km]')
63 ylabel('spektrale Dichte')
64
65 # plot schnitt
66 figure(3)
67 plot(test,'r-')
68
69 show()
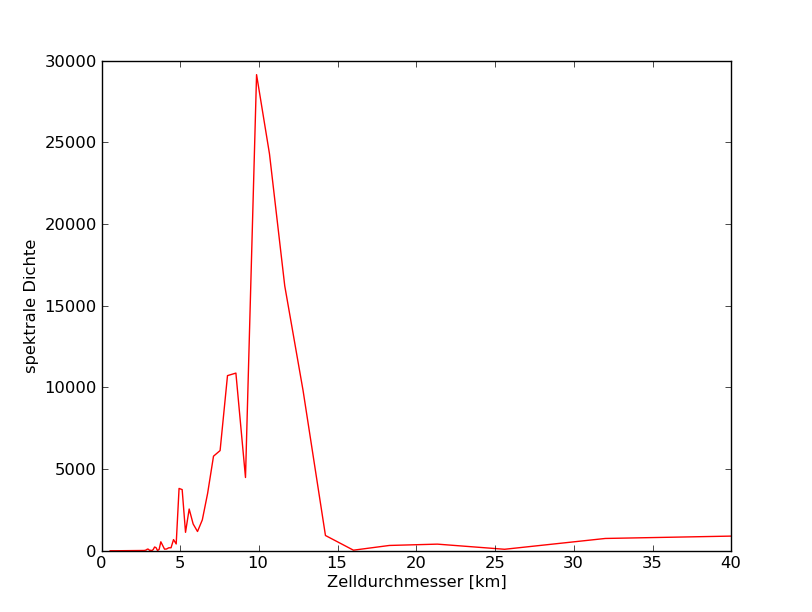
77°N
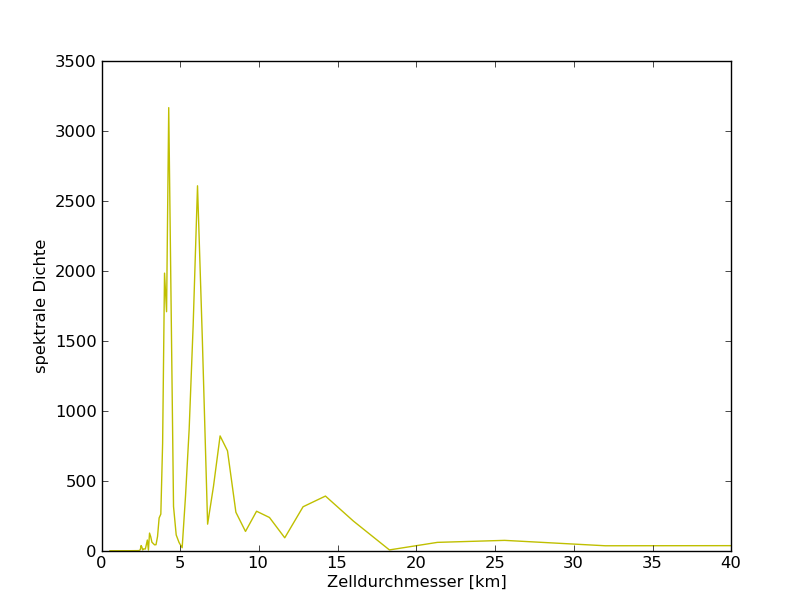
78°N
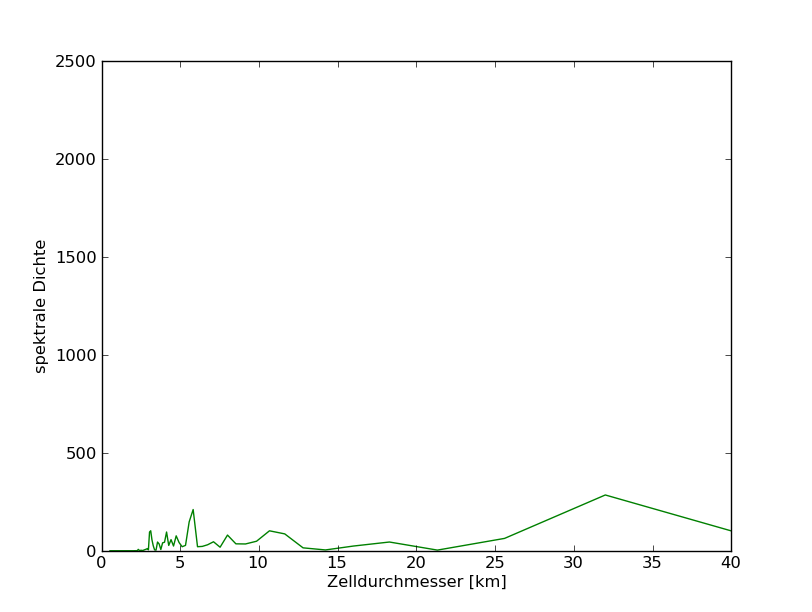
79°N
Zusammenfassung Grenzschicht
Programmcode
1 #!/bin/tcsh
2
3 from pyhdf import SD
4 from pylab import *
5 from mpl_toolkits.basemap import Basemap
6
7 fid=SD.SD('AIRS.2003.03.30.L3.RetStd001.v5.0.14.0.G07215021620.hdf')
8 T=fid.select('Temperature_A')
9 Temp=T.get()
10
11 #Drucklevel
12 Lv=[1000.0,925.0,850.0,700.0,600.0,500.0,400.0,300.0,250.0,200.0,150.0,100.0,
13 70.0, 50.0,30.0, 20.0, 15.0, 10.0, 7.0,5.0, 3.0,2.0,1.5,1.0]
14
15 # Temperaturprofile
16 figure(1)
17 plot(Temp[:,13,187],Lv)
18 ylim((1000.0,1.0))
19 xlim((200.0,280.0))
20 xlabel('T in Kelvin')
21 ylabel('p in hPa')
22 title('used profiles lon=77')
23 show()
24 savefig('Soundings1.png',dpi=75)
25 figure(2)
26 plot(Temp[:,12,184],Lv)
27 ylim((1000.0,1.0))
28 xlim((200.0,280.))
29 xlabel('T in Kelvin')
30 ylabel('p in hPa')
31 title('used profiles lon=78')
32 show()
33 savefig('Soundings2.png',dpi=75)
34 figure(3)
35 plot(Temp[:,11,187],Lv)
36 ylim((1000.0,1.0))
37 xlim((200.0,280.0))
38 xlabel('T in Kelvin')
39 ylabel('p in hPa')
40 title('used profiles lon=79')
41 show()
42 savefig('Soundings3.png',dpi=75)
Profile
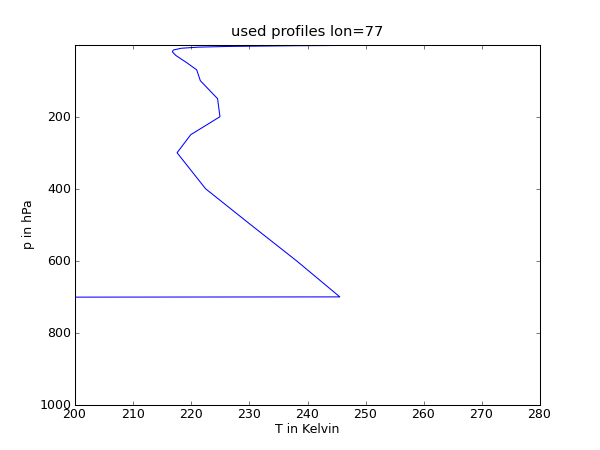
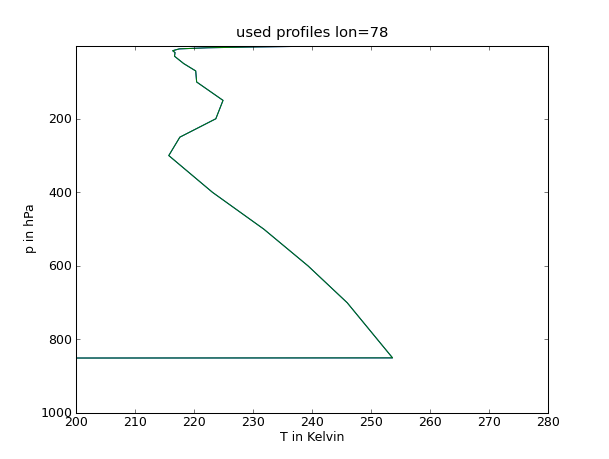
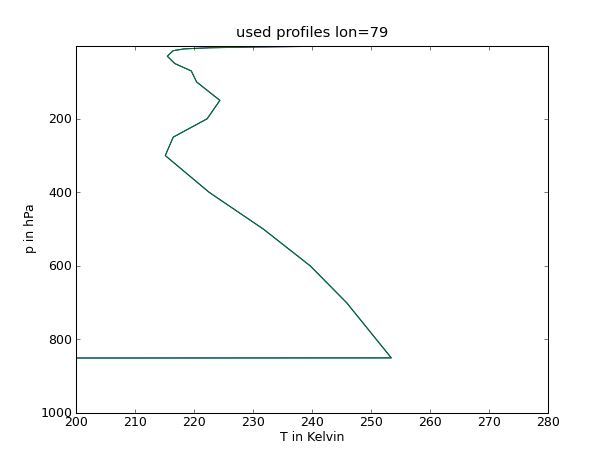
Grenzschichthöhe
Grenzschichtdicke in Meter umrechnen mit barometrischer Höhenformel:
latex error! exitcode was 2 (signal 0), transscript follows:
R=287,1J/kgK
Annahme: T=const. (dadurch wird Grenzschichtdicke unterschätzt)
p=Druckniveau der Wolkenobergrenze
ps=Bodendruck aus Karte
Werte:
Breite |
Dicke in hPa |
Dicke in km |
Zelldurchmesser in km |
Errechnete Dicke in km |
77 |
165 - 315 |
1,2 - 2,6 |
10 |
3,6 |
78 |
90 - 165 |
0,6 - 1,2 |
4 und 6 |
1,4 und 2,1 |
79 |
90 - 165 |
0,6 - 1,2 |
- |
- |
genauere Bestimmung ist aufgrund der groben Auflösung der Drucklevel nicht möglich: Fehler in Größenordnung 1km
Vergleichen mit Theorie
latex error! exitcode was 2 (signal 0), transscript follows:
Im Rahmen der Fehlergenauigkeit von ca. 1km stimmen die Grenzschichtdicken mit der Theorie über ein.