Einführung in die Grundlagen der Numerik und das Programmieren unter Unix/Linux
Vorlesungsmitschrift und Programmcodes von Alexandra Gronholz
Iterative Verfahren zur Bestimmung von Nullstellen
Newton-Verfahren
1 #bisektion
2 from pylab import *
3
4
5 def F(T):
6
7 y=(1-alpha)*S-k*T**4
8 return y
9
10 def Abl(T):
11 ydot=-4*k*T**3
12 return ydot
13
14
15
16 close()
17 alpha=0.3
18 S=1370./4. #[W/m^2]
19 k=5.67e-8 #[W/m^2/K^4]
20 T1=0. #[K]
21 T2=350. #[K]
22 t=linspace(0,300,100)
23 durchlauf=30
24 a,b=0.,350.
25 x=b
26 Texakt=((1.-alpha)*S/k)**(1./4.)
27 diff=zeros(durchlauf)
28 diffnew=zeros(durchlauf)
29
30 figure(1)
31 plot(t,F(t))
32 plot(t,zeros(t.size),'r')
33 title('Strahlungsbilanz')
34 ylabel('Strahlung/Flaeche [W/m^2]')
35 xlabel('Temperatur')
36 show()
37
38
39
40 #nach bisektion
41 for i in range(durchlauf):
42 c=(a+b)/2
43
44 if F(a)*F(c)<=0:
45 b=c
46 else:
47 a=c
48
49 print c
50
51 diff[i]=c-Texakt
52
53 #nach newton:
54 x=x-F(x)/Abl(x)
55 diffnew[i]=x-Texakt
56 print diffnew
57
58
59 figure(2)
60 semilogy(abs(diff),'.-',label='Bisektionsverfahren')
61 plot(abs(diffnew),'g',label='Newton-Raphson-Verfahren')
62 ylabel('Fehlerwert')
63 xlabel('Iterationsschritt')
64 legend()
65 show()
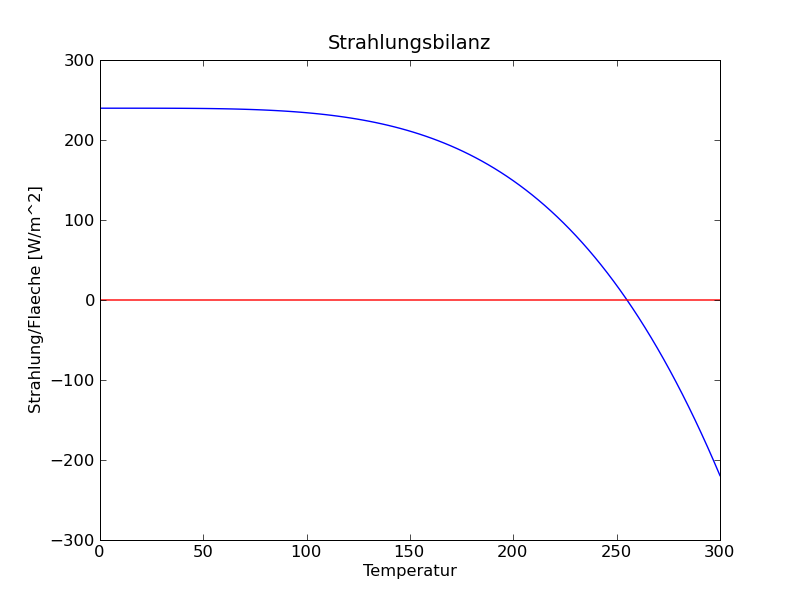
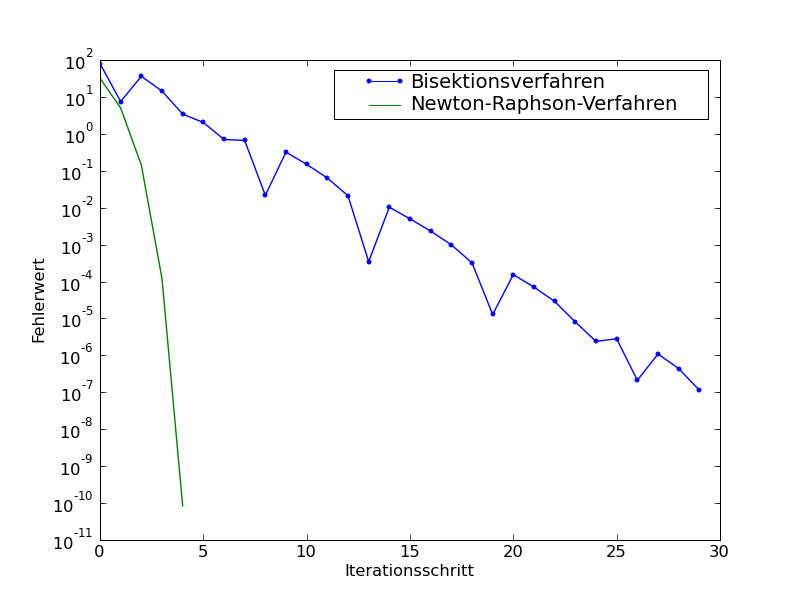 links: STrahlungbilanz rechts: Vergleich Newton-Raphson-Verfahren - Bisektionsverfahren
links: STrahlungbilanz rechts: Vergleich Newton-Raphson-Verfahren - Bisektionsverfahren
Euler-Verfahren
1 from pylab import *
2
3 L=100 #raeumlich
4 M=500 #zeitschritte
5 #c=0.1 #oder unten als sinus def
6 dx=1./L
7 dt=1./10
8 X=linspace(0,1,L)
9 u=zeros((M,L))
10 u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion
11 #u[0,45:55]=1. #rechteck
12
13 ion()
14 figure()
15 line,=plot(X,u[0,:])
16
17 for n in range(M-1):
18
19 c=0.1*cos((n*dt)/10*pi)
20 CFL=c*dt/dx
21 for j in range(L-1):
22 u[n+1,j]=u[n,j]-CFL/2*(u[n,j+1]-u[n,j-1])
23
24 line.set_ydata(u[n+1,:])
25 draw()
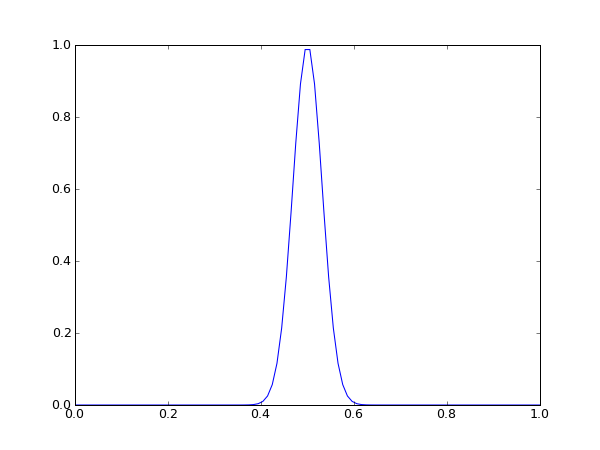
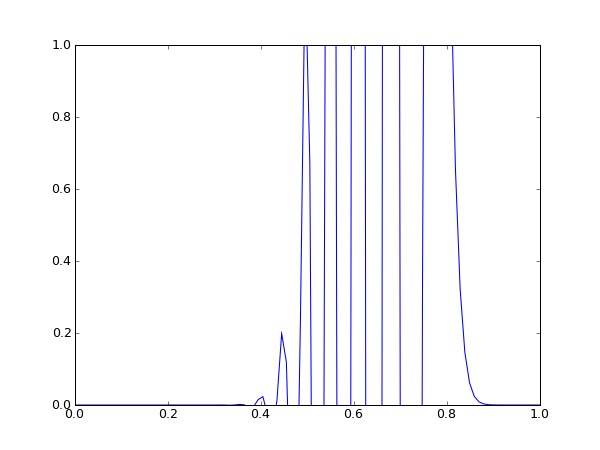 links: Startsituation rechts: Situation nach 50 Zeitschritten
links: Startsituation rechts: Situation nach 50 Zeitschritten
Finite Differenzen Methode zur Lösung der Advektionsgleichung
Upstream-Verfahren
1 from pylab import *
2
3 L=100 #raeumlich
4 M=500 #zeitschritte
5 #c=0.1 #oder unten als sinus def
6 dx=1./L
7 dt=1./10
8 X=linspace(0,1,L)
9 u=zeros((M,L))
10 u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion
11 #u[0,45:55]=1. #rechteck
12
13 ion()
14 figure()
15 line,=plot(X,u[0,:])
16
17 for n in range(M-1):
18
19 c=0.1*cos((n*dt)/10*pi)
20 CFL=c*dt/dx
21 for j in range(L-1):
22 if CFL>0:
23 u[n+1,j]=u[n,j]-CFL*(u[n,j]-u[n,j-1])
24 else:
25 u[n+1,j]=u[n,j]-CFL*(u[n,j+1]-u[n,j])
26
27 line.set_ydata(u[n+1,:])
28 draw()
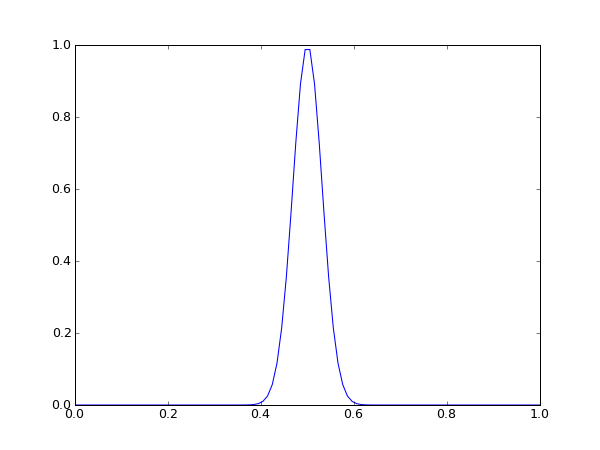
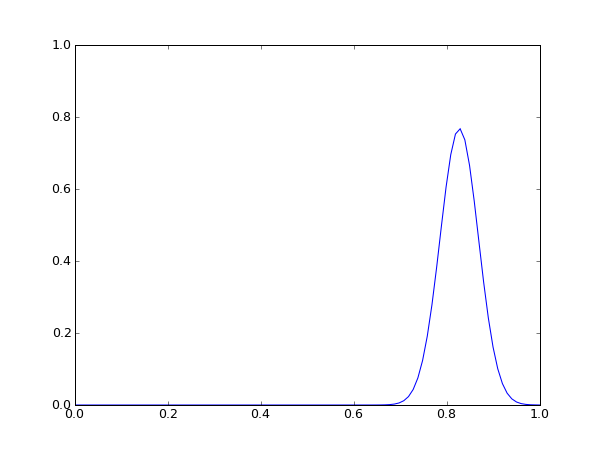
links: Startsituation rechts: Situation nach 50 Zeitschritten
Upstream-Verfahren mit Werteüberschreibung
1 from pylab import *
2
3 L=100 #raeumlich #modifiziert mit ueberschr werten/kein feld mehr
4 M=500 #zeitschritte
5 #c=0.1 #oder unten als sinus def
6 dx=1./L
7 dt=1./10
8 X=linspace(0,1,L)
9 u=zeros((2,L))
10 u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion
11 #u[0,45:55]=1. #rechteck
12
13 ion()
14 figure()
15 line,=plot(X,u[0,:])
16
17 for n in range(M-1):
18
19 c=0.1*cos((n*dt)/10*pi)
20 CFL=c*dt/dx
21 for j in range(L-1):
22 if CFL>0:
23 u[1,j]=u[0,j]-CFL*(u[0,j]-u[0,j-1])
24 else:
25 u[1,j]=u[0,j]-CFL*(u[0,j+1]-u[0,j])
26
27 line.set_ydata(u[1,:])
28 draw()
29 u[0,:]=u[1,:]
Lax-Wendroff-Verfahren
1 from pylab import *
2
3 L=100 #raeumlich
4 M=500 #zeitschritte
5 #c=0.1 #oder unten als sinus def
6 dx=1./L
7 dt=1./10
8 X=linspace(0,1,L)
9 u=zeros((M,L))
10 #u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion
11 u[0,45:55]=1. #rechteck
12
13 ion()
14 figure()
15 line,=plot(X,u[0,:])
16
17 for n in range(M-1):
18
19 c=0.1*cos((n*dt)/10*pi)
20 CFL=c*dt/dx
21 for j in range(L-1):
22 u[n+1,j]=u[n,j]-CFL/2*(u[n,j+1]-u[n,j-1])+CFL**2/2*(u[n,j+1]-2*u[n,j]+u[n,j-1])
23
24 line.set_ydata(u[n+1,:])
25 draw()
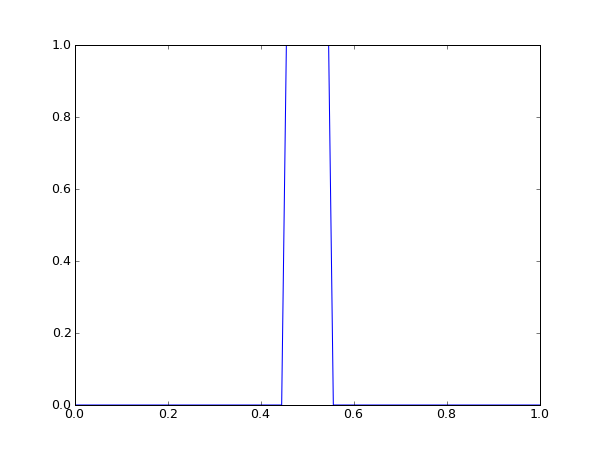
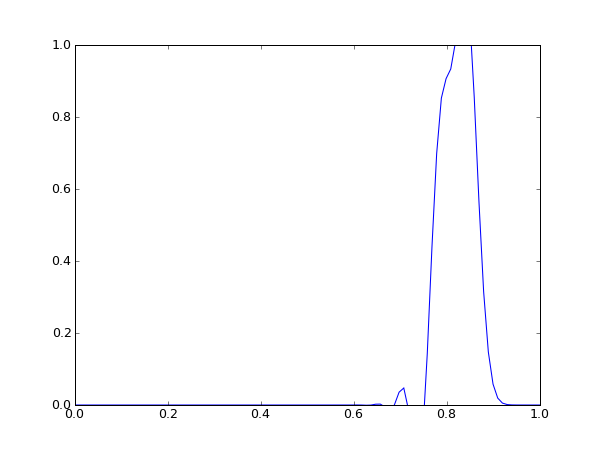 links: Startsituation rechts: Situation nach 50 Zeitschritten
links: Startsituation rechts: Situation nach 50 Zeitschritten
Leapfrog-Verfahren
1 from pylab import *
2
3 L=100 #raeumlich
4 M=500 #zeitschritte
5 #c=0.1 #oder unten als sinus def
6 dx=1./L
7 dt=1./10
8 X=linspace(0,1,L)
9 u=zeros((M,L))
10 u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion
11 #u[0,45:55]=1. #rechteck
12
13 ion()
14 figure()
15 line,=plot(X,u[0,:])
16
17 c=0.1*cos((0*dt)/10*pi)
18 CFL=c*dt/dx
19
20
21 for j in range(L-1): #j=raum
22 u[1,j]=u[0,j]-CFL/2*(u[0,j+1]-u[0,j-1])+CFL**2/2*(u[0,j+1]-2*u[0,j]+u[0,j-1])
23
24 for n in range(1,M-1):
25
26 c=0.1*cos((n*dt)/10*pi)
27 CFL=c*dt/dx
28
29
30 for j in range(L-1):
31 u[n+1,j]=u[n-1,j]-CFL*(u[n,j+1]-u[n,j-1])
32
33 line.set_ydata(u[n+1,:])
34 draw()
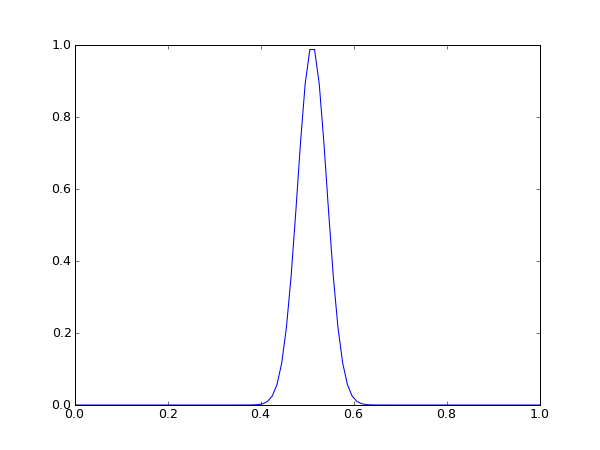
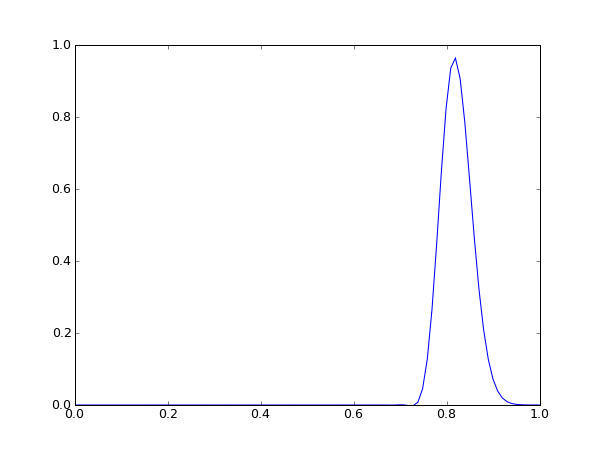 links: Startsituation rechts: Situation nach 50 Zeitschritten
links: Startsituation rechts: Situation nach 50 Zeitschritten
FAZIT
Das Eulerverfahren zeit starke Instabilität. Während das Upstream-Verfahren zwar stabiler ist als das Euler-Verfahren (sofern CFL-Bedingung erfüllt), zeigt es dennoch starke Diffusion. Das Lax-Wendroff-Verfahren ist weniger diffusiv als das Upstrem-Verfahren und das Leapfrog-Verfahren zeigt keine Diffusion mehr, dafür jedoch starke Dispersion.
Ozeanische Grenzschicht
1 from pylab import *
2
3 h=10. #Deckschichtdicke in [m]
4 Cp=4000. #Waermekapazitaet Ozean in [J/Kg/K]
5 S=30. #bei Salzgehalt von...
6 d=1000 #Anzahl der Durchlaeufe
7 T=zeros(d) #bei Temp von...
8 T[0]=10 #Startwert Temperatur
9 dt=60*60*24 #Zeitschritteneinheiten [s]-->Tage mit 60*60*24
10 start=0 #zeitlicher Startwert
11 #ti=a=r_[start:d:dt] #array mit Zeitpunkten
12 alph=0.06 #Albedowert Wasser
13 epsi=0.97 #Emissivitaet
14 sig=5.67e-8 #Boltzmannkonstante
15 I=375 #Einstrahlung in [W/m2]-->375: Gleichgewichtswert
16 rho=1024
17
18
19 for i in range(d-1):
20 T[i+1]=T[i]+((((1-alph)*I-epsi*sig*(T[i]+273)**4)*dt)/(h*Cp*rho))
21
22 plot(T)
23 xlabel('Zeit in Tagen')
24 ylabel(r'Temperatur in $^\circ$C')
25 title('Energiebilanz der ozeanischen Grenzschicht')
26 show()
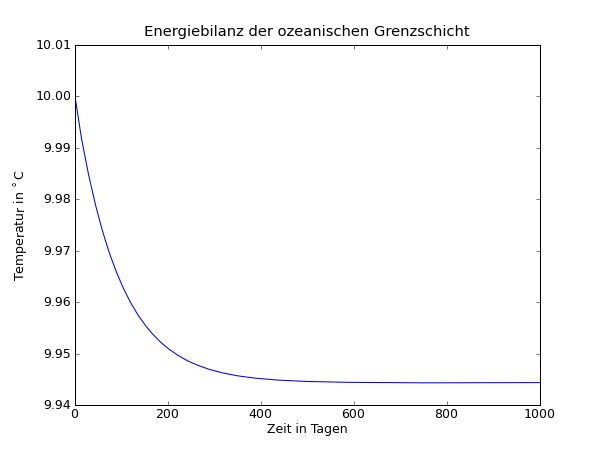
Ozeanische Grenzschicht in Fortran
program ozean
implicit none !damit variablen nicht vordefiniert
integer, parameter :: d=1000 !Anzahl der Durchlaeufe, + als PARAMETER wenn spaeter nochmal benutzt
real :: T(0:d-1) !automatisch Nullen
real :: h,Cp,S,dt,alph,epsi,sig,I,rho
integer :: j ! nicht 2mal I, da keine unterscheidung in GROSS U KLEIN!
h=10. !Deckschichtdicke in [m]
Cp=4000. !Waermekapazitaet Ozean in [J/Kg/K]
S=30. !bei Salzgehalt von...
T(0)=10. !Startwert Temperatur
dt=60*60*24. !Zeitschritteneinheiten [s]-->Tage mit 60*60*24
alph=0.06 !Albedowert Wasser
epsi=0.97 !Emissivitaet
sig=5.67e-8 !Boltzmannkonstante
I=375. !Einstrahlung in [W/m2]-->375: Gleichgewichtswert
rho=1024.
do j=0,d-1
T(j+1)=T(j)+((((1-alph)*I-epsi*sig*(T(j)+273)**4)*dt)/(h*Cp*rho))
end do
print*, T(d-1)
end program ozean
!Informationen zum Erzeugen:
!a) zum kompilieren 'gfortran + name.f90'
!erzeugt a.out
!b) ./a.out oder
! (ganzer weg) ohne './' (finde ueber pwd)