|
Size: 1115
Comment:
|
Size: 2630
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 11: | Line 11: |
| === Upstream-Verfahren === | |
| Line 46: | Line 46: |
| links: Startsituation rechts: Endsituation |
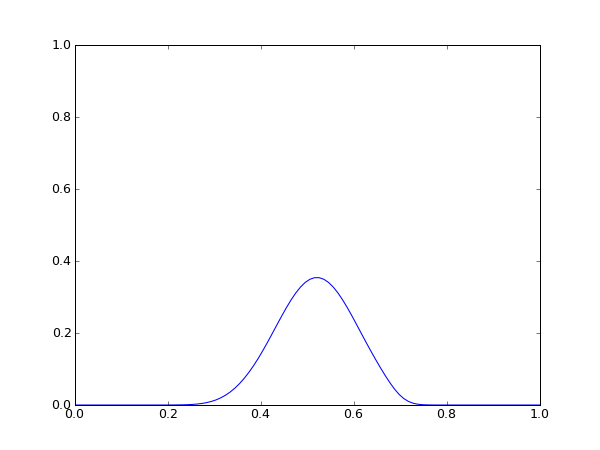
'''links:''' Startsituation '''rechts:''' Endsituation === Upstream-Verfahren mit Werteüberschreibung === {{{#!python from pylab import * L=100 #raeumlich #modifiziert mit ueberschr werten/kein feld mehr M=500 #zeitschritte #c=0.1 #oder unten als sinus def dx=1./L dt=1./10 X=linspace(0,1,L) u=zeros((2,L)) u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion #u[0,45:55]=1. #rechteck ion() figure() line,=plot(X,u[0,:]) for n in range(M-1): c=0.1*cos((n*dt)/10*pi) CFL=c*dt/dx for j in range(L-1): if CFL>0: u[1,j]=u[0,j]-CFL*(u[0,j]-u[0,j-1]) else: u[1,j]=u[0,j]-CFL*(u[0,j+1]-u[0,j]) line.set_ydata(u[1,:]) draw() u[0,:]=u[1,:] }}} === Leapfrog-Verfahren === {{{#!python from pylab import * L=100 #raeumlich M=500 #zeitschritte #c=0.1 #oder unten als sinus def dx=1./L dt=1./10 X=linspace(0,1,L) u=zeros((M,L)) u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion #u[0,45:55]=1. #rechteck ion() figure() line,=plot(X,u[0,:]) c=0.1*cos((0*dt)/10*pi) CFL=c*dt/dx for j in range(L-1): #j=raum u[1,j]=u[0,j]-CFL/2*(u[0,j+1]-u[0,j-1])+CFL**2/2*(u[0,j+1]-2*u[0,j]+u[0,j-1]) for n in range(1,M-1): c=0.1*cos((n*dt)/10*pi) CFL=c*dt/dx for j in range(L-1): u[n+1,j]=u[n-1,j]-CFL*(u[n,j+1]-u[n,j-1]) line.set_ydata(u[n+1,:]) draw() }}} {{attachment:leapfro_start.png}} |
Einführung in die Grundlagen der Numerik und das Programmieren unter Unix/Linux
Iterative Verfahren zur Bestimmung von Nullstellen
Finite Differenzen Methode zur Lösung der Advektionsgleichung
Upstream-Verfahren
1 from pylab import *
2
3 L=100 #raeumlich
4 M=500 #zeitschritte
5 #c=0.1 #oder unten als sinus def
6 dx=1./L
7 dt=1./10
8 X=linspace(0,1,L)
9 u=zeros((M,L))
10 u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion
11 #u[0,45:55]=1. #rechteck
12
13 ion()
14 figure()
15 line,=plot(X,u[0,:])
16
17 for n in range(M-1):
18
19 c=0.1*cos((n*dt)/10*pi)
20 CFL=c*dt/dx
21 for j in range(L-1):
22 if CFL>0:
23 u[n+1,j]=u[n,j]-CFL*(u[n,j]-u[n,j-1])
24 else:
25 u[n+1,j]=u[n,j]-CFL*(u[n,j+1]-u[n,j])
26
27 line.set_ydata(u[n+1,:])
28 draw()
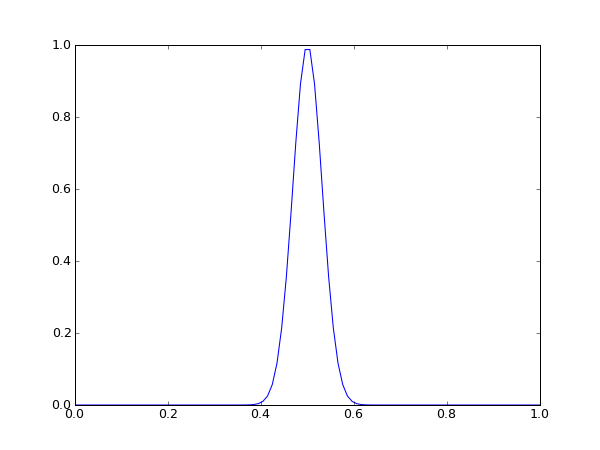
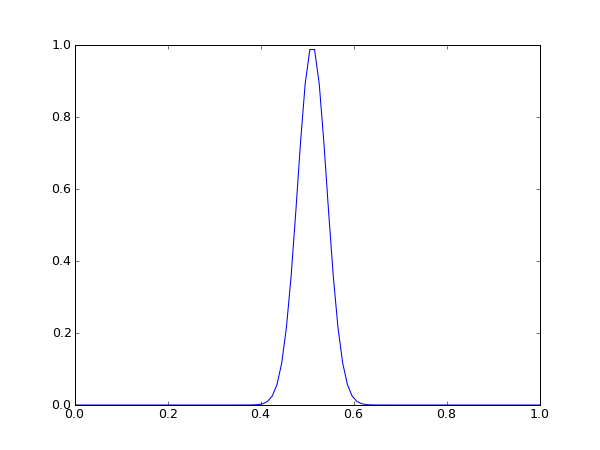
links: Startsituation rechts: Endsituation
Upstream-Verfahren mit Werteüberschreibung
1 from pylab import *
2
3 L=100 #raeumlich #modifiziert mit ueberschr werten/kein feld mehr
4 M=500 #zeitschritte
5 #c=0.1 #oder unten als sinus def
6 dx=1./L
7 dt=1./10
8 X=linspace(0,1,L)
9 u=zeros((2,L))
10 u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion
11 #u[0,45:55]=1. #rechteck
12
13 ion()
14 figure()
15 line,=plot(X,u[0,:])
16
17 for n in range(M-1):
18
19 c=0.1*cos((n*dt)/10*pi)
20 CFL=c*dt/dx
21 for j in range(L-1):
22 if CFL>0:
23 u[1,j]=u[0,j]-CFL*(u[0,j]-u[0,j-1])
24 else:
25 u[1,j]=u[0,j]-CFL*(u[0,j+1]-u[0,j])
26
27 line.set_ydata(u[1,:])
28 draw()
29 u[0,:]=u[1,:]
Leapfrog-Verfahren
1 from pylab import *
2
3 L=100 #raeumlich
4 M=500 #zeitschritte
5 #c=0.1 #oder unten als sinus def
6 dx=1./L
7 dt=1./10
8 X=linspace(0,1,L)
9 u=zeros((M,L))
10 u[0,:]=exp(-500*(X-0.5)**2) #gaussfunktion
11 #u[0,45:55]=1. #rechteck
12
13 ion()
14 figure()
15 line,=plot(X,u[0,:])
16
17 c=0.1*cos((0*dt)/10*pi)
18 CFL=c*dt/dx
19
20
21 for j in range(L-1): #j=raum
22 u[1,j]=u[0,j]-CFL/2*(u[0,j+1]-u[0,j-1])+CFL**2/2*(u[0,j+1]-2*u[0,j]+u[0,j-1])
23
24 for n in range(1,M-1):
25
26 c=0.1*cos((n*dt)/10*pi)
27 CFL=c*dt/dx
28
29
30 for j in range(L-1):
31 u[n+1,j]=u[n-1,j]-CFL*(u[n,j+1]-u[n,j-1])
32
33 line.set_ydata(u[n+1,:])
34 draw()