die Besprechung ergab fuer diese Gruppe:
- Trockenprogrammierung: insbesondere die Konsistenz von Bildkoordinaten von ASAR und Freibord-Footprint klären die Klasseneinteilungen von ASAR und Freibordhöhen vergleichen Frage "welche Statistik will man anwenden" beantworten
Dienstag
Am Dienstag / Mittwoch erzeugtes Programm, das mit dem Zufallsgenerator sowohl die ASAR als auch Freibord - Daten erzeugt:
1 #project_plot.py
2
3 from pylab import *
4 from scipy import *
5 import time,calendar,os,pipes,struct,string
6 import random
7 import scipy.ndimage as ndi
8 from matplotlib.patches import Ellipse
9
10 nk=5 #number of classes
11 ndim=[1000,1000] #dimension of ASAR image in pixels
12 res=12.5
13 freeb_asar_pixels=int(60./res)# footprint of freeboard is 60m
14
15 fx0,fy0,fx2,fy2=[0.2,1.,1.,0.1]
16 fx0,fy0,fx2,fy2=fx0*ndim[0],fy0*ndim[0],fx2*ndim[0],fy2*ndim[0] # freeboard coordinates from input file
17 dist=sqrt((fx2-fx0)**2+(fy2-fy0)**2)*res
18 fdist=172 #distance of two freeboard footprints is 172m
19 nf=int(dist/fdist)
20
21 fz_h=zeros(nf) #fz_h is the freeboard heights
22 # produce a random array of freeboard heights
23 for i in range(nf):
24 fz_h[i]=random.random()*70
25
26 # the x,y positions of the freeboard footprints
27 if fx2==fx0:
28 fx=zeros(nf)+fx0
29 fy=linspace(0,ndim[1],nf)
30 else:
31 teta=(fy2-fy0)/(fx2-fx0)
32 fx=linspace(fx0,fx2,nf)
33 fy=(fx-fx0)*teta+fy0
34
35 #produce a random matrix of ASAR image classes (in 5 classes)
36 a=zeros((ndim[0],ndim[1]))
37 for i in range(ndim[0]):
38 for j in range(ndim[1]):
39 a[i,j]=int(random.random()*(nk)+1)
40
41 #tranform from float to int
42 B=a.astype(int)
43
44 #select the class of footprints from ASAR Image
45 fz=zeros(nf)
46 for i in range(nf):
47 fz[i]=B[int(fx[i]-1),int(fy[i]-1)]
48
49 #calculation of mean and standard deviation of freeboard heights in each class
50 mean=zeros(nk)
51 std_kl=zeros(nk)
52 for kl in range(1,6):
53 s=(fz==kl)
54 fh_kl=fz_h[s]
55 mean[kl-1]=fh_kl.sum()/fh_kl.shape[0]
56 std_kl[kl-1]=std(fh_kl)
57
58 #plot mean and error bar
59 kl=arange(nk)+1
60 bar(kl,mean,yerr=std_kl,ecolor='r',align='center')
61 axis('tight')
62 savefig('kl_mean_std', orientation='portrait', format='png')
63
64 #calculate correlation coefficient
65 #corr=xcorr(fz,fz_h,normed=True)[1][nf]
66
67 figure()
68 #plot ASAR image class together with freeboard heights
69 x=arange(nf)
70 bar(x,fz,width=0.3,align='center')
71 ylim(0,10)
72 ax=twinx()
73 plot(x,fz_h,'r+-',ms=10,linewidth=1)
74 ylim(0,70)
75 savefig('asar_fb', orientation='portrait', format='png')
76
77 #axis('tight')
78
79 #plot ASAR image with freeboard flight
80 figure()
81 ct=zeros((nf,4))
82 for i in range(nf):
83 ct[i]=cm.gist_rainbow(int(fz_h[i]))
84 ax=axes()
85 ells=[Ellipse(xy=[fx[i],fy[i]],width=freeb_asar_pixels,height=freeb_asar_pixels) for i in xrange(nf)]
86 n=0
87 for e in ells:
88 ax.add_artist(e)
89 e.set_clip_box(ax.bbox)
90 e.set_alpha(0.5)
91 e.set_facecolor(ct[n])
92 n+=1
93 gray()
94 imshow(B,origin='lower',interpolation=None)
95 hold(True)
96 #plot(fx,fy,'r+-',linewidth=2)
97 xlim(400,600)
98 ylim(500,700)
99 #xlim(0,1000)
100 #ylim(0,1000)
101 colorbar()
102 savefig('asar_fb_track', orientation='portrait', format='png')
103
104 #figure()
105 #imshow(a)
106 show()
Figure 1 (class - mean, standard deviation) / VIRTUELLE DATEN :
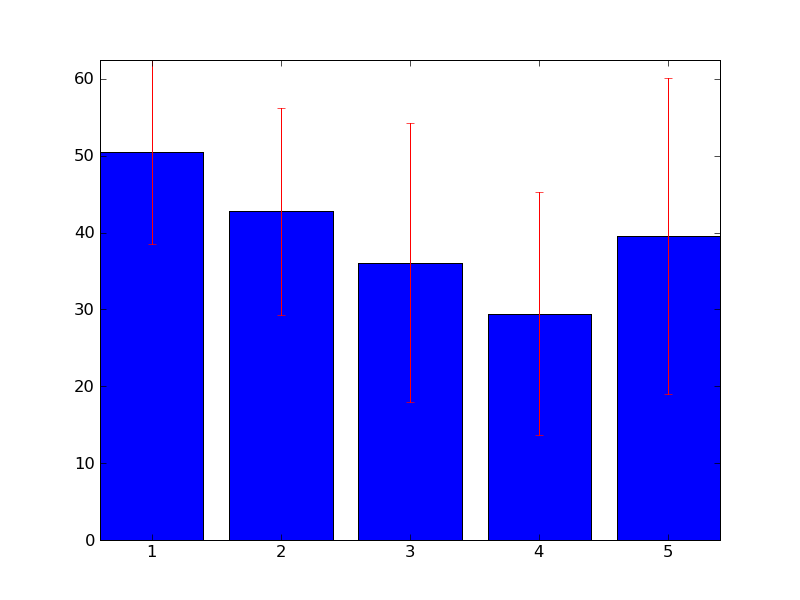
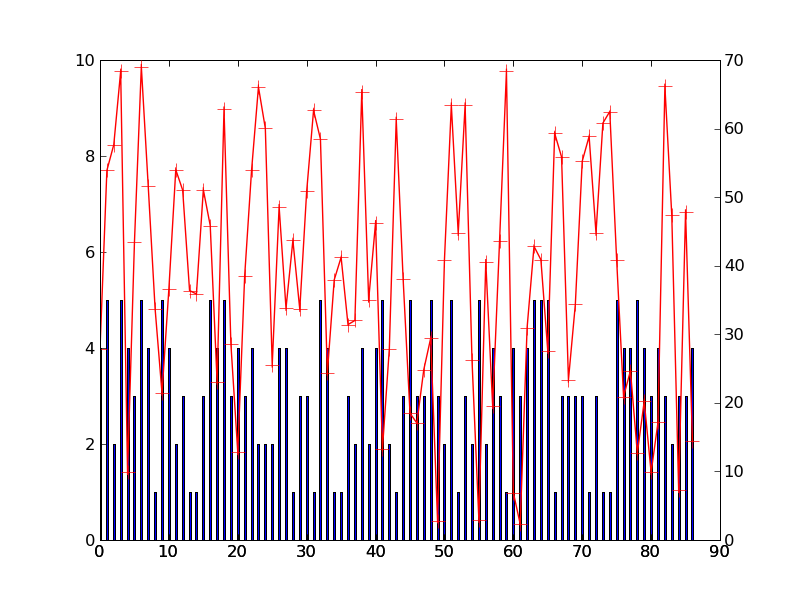
Figure 2 (asar, freboard) / VIRTUELLE DATEN :
Ziele für Mittwoch:
- Vom gestern erzeugte Graphen verfeinen
Programm für ASAR-Rohdaten & Freiborddaten Vergleich
Mittwoch
Am Mittwoch erzeugtes Programm, das ASAR-Rohdaten und Freiborddaten (Zufallsgenerator), Faltungmaske 5x5 Pixel wurde benutzt:
1 #ASAR_raw.py
2
3 from pylab import *
4 from scipy import *
5 import time,calendar,os,pipes,struct,string
6 import random
7 import scipy.ndimage as ndi
8 from read_asar import *
9
10 filename='/pf/u/u242027/SAR_raw/ASA_IMP_1PNDPA20060617_043346_000000162048_00362_22460_2136.N1'
11 I=read_asar_imp(filename)
12
13 ndim=[1000,1000] #dimension of ASAR image in pixels
14
15 fx0,fy0,fx2,fy2=[200.,1000.,1000.,100.] # freeboard coordinates from input file
16 cellsize=12.5 #12.5m pixelsize
17 dist=sqrt((fx2-fx0)**2+(fy2-fy0)**2)*cellsize
18 fdist=172 #distance of two freeboard footprints is 172m
19 nf=dist/fdist
20
21 fz_h=zeros(nf) #fz_h is the freeboard heights
22 # produce a random array of freeboard heights
23 for i in range(nf):
24 fz_h[i]=random.random()*70
25
26 # the x,y positions of the freeboard footprints
27 if fx2==fx0:
28 fx=zeros(nf)+fx0
29 fy=linspace(0,ndim[1],nf)
30 else:
31 teta=(fy2-fy0)/(fx2-fx0)
32 fx=linspace(fx0,fx2,nf)
33 fy=(fx-fx0)*teta+fy0
34
35
36 B=I[1000:2000,1000:2000]
37
38 mask=array(([1,1,1,1,1],[1,2,2,2,1],[1,2,3,2,1],[1,2,2,2,1],[1,1,1,1,1]))/35.
39 C=ndimage.convolve(B,mask,mode='reflect')
40
41 #select the intensity value of footprints from ASAR Image
42 fz=zeros(nf)
43 for i in range(nf):
44 pos=[int(fx[i]-1),int(fy[i]-1)]
45 fz[i]=B[pos[0],pos[1]]
46
47
48 #calculate correlation coefficient
49 corr=xcorr(fz,fz_h,normed=True)[1][nf]
50
51 figure()
52 #plot ASAR image intensity together with freeboard heights
53 x=arange(int(nf))
54 plot(x,fz,'b+-')
55 ax=twinx()
56 plot(x,fz_h,'r+-')
57 savefig('asar_fb_track_RAW', orientation='portrait', format='png')
58
59 #plot ASAR image with freeboard flight
60 #figure()
61 #plot(fx,fy,'r+-',linewidth=2)
62 #colorbar()
63 #imshow(B,origin='lower',interpolation=None)
64 #hold(True)
65
66 show()
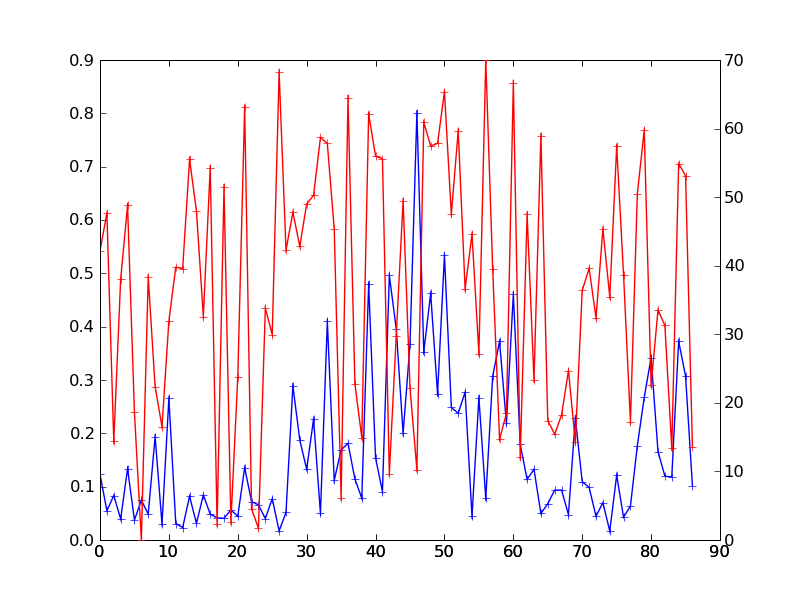
Figure 1 (raw asar image, freeboard) / REELLE ASAR DATEN + VIRTUELLER FREIBORDDATENSATZ ::
Ziele für Donnerstag:
- Farbtabelle für Freibordhöhen einbauen
- Programpaketen der anderen Gruppe übernehmen und ins Programm einbauen
- Testen und erste Ergebnisse liefern
- Bericht schreiben
Donnerstag
Am Donnerstag erzeugte Farbtabelle im 'project_plot.py' Program für Freibordhöhen:
Figure 3 (asar, freeboard track) / VIRTUELLE DATEN :
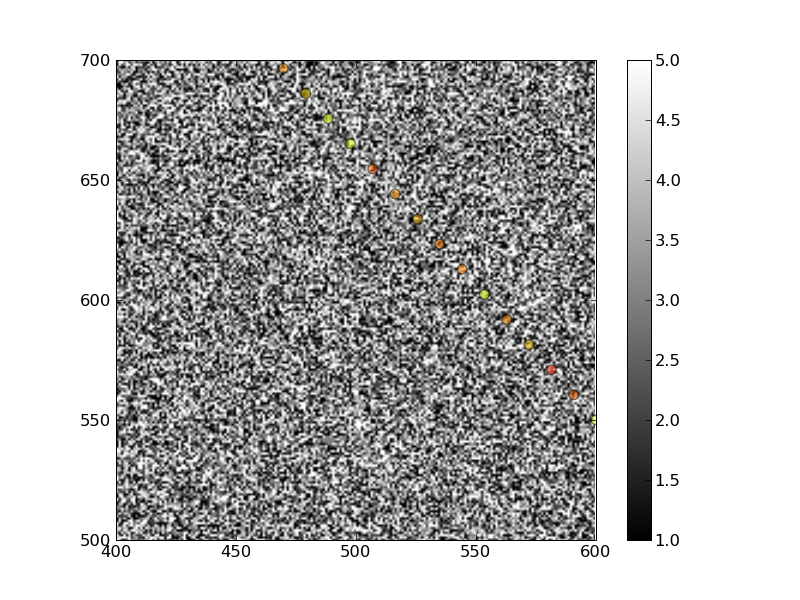
vergleichen Frage "welche Statistik will man anwenden" beantworten
Freitag
Am Freitag wurden die Teilprogramme zusammengesetzt und das Hauptprogram geschrieben. Die Bericht wurde geschrieben.
Program "results.py" nimmt als input die Freibordposition (fx,fy), Freibordhöhe (fz_h) und das klassifizierte ASAR Bild an.:
1 #results.py
2 from pylab import *
3 from scipy import *
4 import time,calendar,os,pipes,struct,string
5 import random
6 import scipy.ndimage as ndi
7 from matplotlib.patches import Ellipse
8
9
10
11 def results(fx,fy,fz_h,B):
12 nk=B.max() #number of classes
13 ndim=B.shape
14 fx=fx*ndim[0]
15 fy=fy*ndim[1]
16 nf=fx.shape[0]
17 res=12.5
18 freeb_asar_pixels=int(60./res)# footprint of freeboard is 60m
19 #select the class of footprints from ASAR Image
20 fz=zeros(nf)
21 for i in range(nf):
22 fz[i]=B[int(fx[i]-1),int(fy[i]-1)]
23
24 #calculation of mean and standard deviation of freeboard heights in each class
25 mean=zeros(nk)
26 std_kl=zeros(nk)
27 for kl in range(nk):
28 s=(fz==kl)
29 fh_kl=fz_h[s]
30 mean[kl]=fh_kl.sum()/fh_kl.shape[0]
31 std_kl[kl]=std(fh_kl)
32
33 #plot mean and error bar
34 kl=arange(nk)
35 bar(kl,mean,yerr=std_kl,ecolor='r',align='center')
36 axis('tight')
37 savefig('kl_mean_std.png', orientation='portrait', format='png')
38
39 #calculate correlation coefficient
40 #corr=xcorr(fz,fz_h,normed=True)[1][nf]
41
42 figure()
43 #plot ASAR image class together with freeboard heights
44 x=arange(nf)
45 bar(x,fz,width=0.3,align='center')
46 ax=twinx()
47 plot(x,fz_h,'r+-',ms=10,linewidth=1)
48 savefig('asar_fb.png', orientation='portrait', format='png')
49
50 #axis('tight')
51
52 #plot ASAR image with freeboard flight
53 figure()
54 ct=zeros((nf,4))
55 for i in range(nf):
56 ct[i]=cm.gist_rainbow(int(fz_h[i]))
57 ax=axes()
58 ells=[Ellipse(xy=[fx[i],fy[i]],width=freeb_asar_pixels,height=freeb_asar_pixels) for i in xrange(nf)]
59 n=0
60 for e in ells:
61 ax.add_artist(e)
62 e.set_clip_box(ax.bbox)
63 e.set_alpha(0.5)
64 e.set_facecolor(ct[n])
65 n+=1
66 gray()
67 imshow(B,origin='lower',interpolation=None)
68 hold(True)
69 #plot(fx,fy,'r+-',linewidth=2)
70 colorbar()
71 savefig('asar_fb_track.png', orientation='portrait', format='png')
72
73 #figure()
74 #imshow(a)
75 show()
HAUPTPROGRAM "project_woche.py", das die Module aller Gruppen aufruft und durchführt:
1 #project_woche.py
2
3 import read_fh
4 import asar_kl
5 from results import *
6 from pylab import *
7 from scipy import *
8 import time,calendar,os,pipes,struct,string
9 import scipy.ndimage as ndi
10 from matplotlib.patches import Ellipse
11
12 filename1='/pf/u/u242027/ASA_IMP_1PNDPA20060617_043346_000000162048_00362_22460_2136.N1'
13 filename2='/pf/u/u242027/LonLatFre_1706_6.xyz'
14 filename3='/pf/u/u241110/project/asar_class_filtered_1090x1051.dat'
15
16 fx,fy,fz_h=read_fh.fit_freeboard_ASAR(filename1,filename2)
17 ndim=[1090,1051] #dimension of ASAR image in pixels
18 B=reshape(fromfile(filename3),(ndim[0],ndim[1]))
19 results(fx,fy,fz_h,B)
Figure 1 (class - mean, standard deviation) / REELLE DATEN :
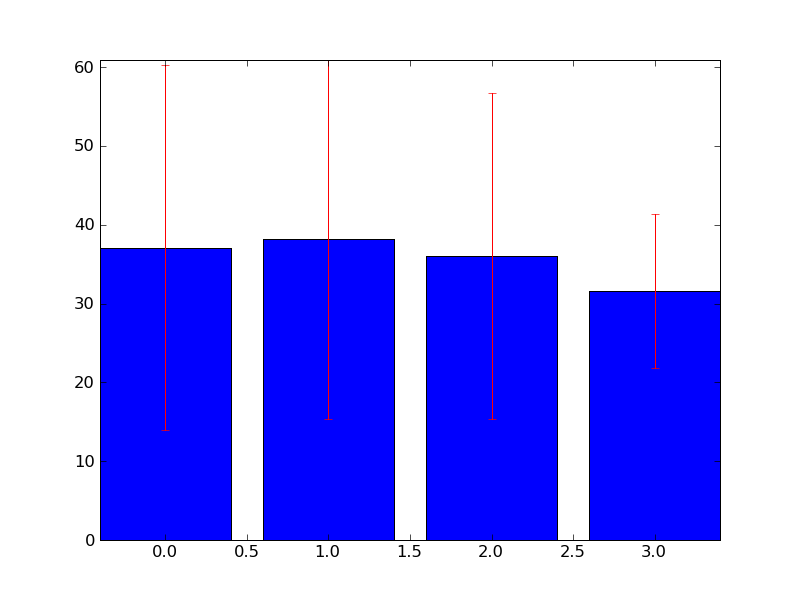
Figure 2 (asar, freboard) / REELLE DATEN :
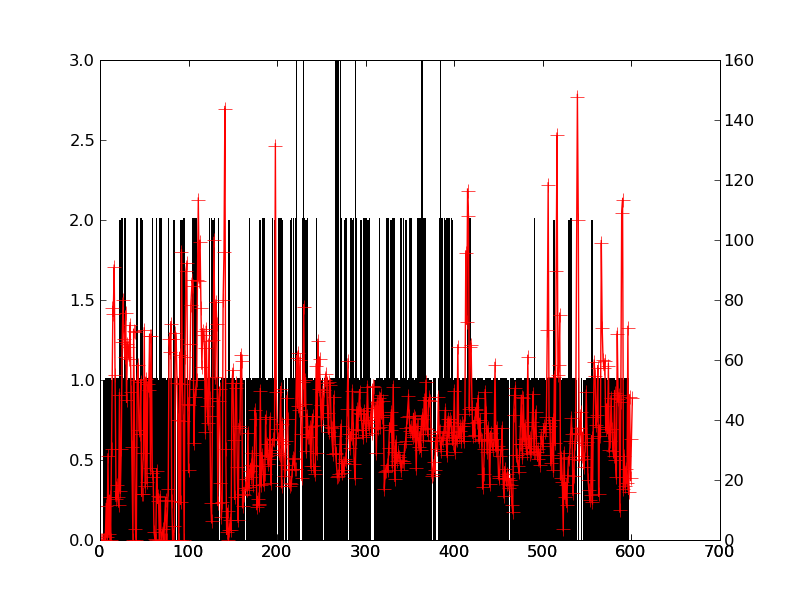
Figure 3 (asar, freeboard track) / REELE DATEN :
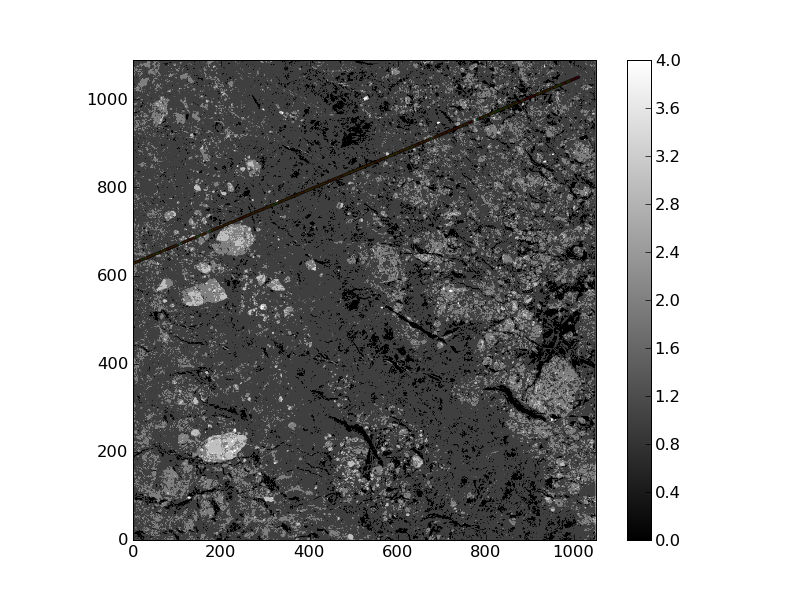
- Berichtteil (Zusammenbau):
Motivation
Das Ziel von unserem Projekt ist die Klassifikation der Freibordhöhen im Gebiet des Weddellmeeres (Antarktis). Dazu stehen uns ICESat und ENVISAT Daten zur Verfügung. Unsere Aufgabenstellung besteht darin festzustellen, ob es möglich ist, die ASAR Daten für eine Eisdickenklassifikation benutzen zu können. Die ICESat Überflugsdaten werden bei der Validierung helfen.Des weiteren fragen wir uns, im welchem Fehlerbereich diese Klassifikation möglich ist.
Daten
In der erste Phase unseres Projektes haben wir mit Daten gearbeitet, die mit dem Zufallsgenerator erzeugt worden sind. Später haben wir die Programme anderer Gruppen eingebaut, dessen Eingabe a) die Freibordhöhen in den Bildkoordinaten und b) das Array der klassifizierten ASAR Datei war.
Methodik (Arbeitsschritten, Theorie, Input/Output)
Als erste Aufgabe haben wir uns damit beschäftigt, wie man den Zufallsgenerator benutzen kann. Mittels der Funktion "random()" haben wir das klassifizierte ASAR-Testbild (1000x1000 Pixels, 12,5 Meter Pixelgröße) mit dem simulierten ICESat-Überflug erzeugt. Das klassifizierte ASAR-Bild enthältet 5 Klassen (nk), die als dritte Dimension zu der Bildkoordinate zugehört (fx,fy,Klasse). Der ICESat-Überflug bestand aus Punkten mit Abständen von 172 Meter, wobei nur die erste und letzte Koordinate (fx0,fy0,fx2,fy2) normiert (0-1) eingegeben wird. Die normierte Koordinaten haben wir mit der Dimension (1000x1000) multipliziert um die Freibordpunkte in den richtigen Bildkoordinaten zu bekommen. Aus der Distanz zwischen dem ersten und letzten Punk haben wir bei dem bekannten Abstand die Punktenzahl (nf) berechnet.
Es wurden nur die unter Freibordpunkten liegenden ASAR-Klassen (fz) in der Korrelationsberechnung berücksichtigt und anschließend der Mittelwert und die Standardabweichung für die Freibordhöhe in jeder Klasse berechnet (siehe unterliegende Bild). 
Danach haben wir die Teilprogramme von den anderen Gruppen erhalten.
Ergebnisse (Output, Statistik)
Figure 1 (class - mean, standard deviation) / REELLE DATEN :

Figure 2 (asar, freboard) / REELLE DATEN :

Figure 3 (asar, freeboard track) / REELE DATEN :

Diskussion
- Hypothese: "Es ist möglich die Eisdicke/Freibordhöhe mittels ASAR Daten zu klassifizieren."
- "Die ICESat Daten werden uns dabei helfen, die klassifizierte Bilder zu validieren."
- Im welchem Fehlerbereich diese Klassifikation möglich ist?