Arbeitsgruppe 1: Freibord
Die Aufgabe der Arbeitsgruppe bestand darin, die I
Daten
Der Gruppe stand ein ASAR-Satellitenbild zur Verfügung, das einen Auschnitt des Weddellmeeres zeigt und ein ICESat-Datensatz, der die geographischen Positionen (lon, lat) und die an diesen Punkten gemessenen Freibordhöhen (cm) für einen Überflug quer durch den ASAR-Ausschnitt beinhaltet.
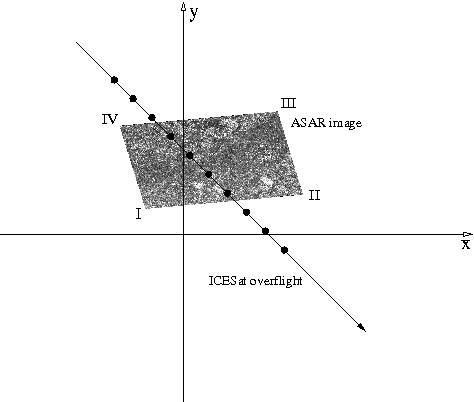
Methodik
Theorie zur Koordinatentransformation:
Eine affine Abbildung ist eine lineare Koordinatentransformation, die die elementaren Transformationen Translation, Rotation, Dilatation, Stauchung und Scherung umfasst. Sie kann durch Vektoraddition und Matrixmultiplikation ausgedrueckt werden:
latex error! exitcode was 2 (signal 0), transscript follows:
Homogene Koordinaten:
latex error! exitcode was 2 (signal 0), transscript follows:
Für drei nichtkollineare Punkte ergibt sich damit folgendes Gleichungssystem:
latex error! exitcode was 2 (signal 0), transscript follows:
oder
latex error! exitcode was 2 (signal 0), transscript follows:
Die Transformationsmatrix A für drei nichtkollineare Punkte lässt sich dann einfach aus
latex error! exitcode was 2 (signal 0), transscript follows:
bestimmen.
Transformationskoeffizienten für mehr als drei nichtkollineare Punkte erhält man mit der Methode der kleinsten Quadrate aus:
latex error! exitcode was 2 (signal 0), transscript follows:
(für mehr Informationen siehe B. Jähne, Digitale Bildverarbeitung, Kapitel 10.4)
Arbeitsschritte:
Die Gruppe hat Programme bzw. Funktionen erarbeitet, die folgendes tun:
- Einlesen der ICESat-Datei und umrechnen der geographischen Koordinaten des Ueberfluges in polarstereographische Koordinaten.
- Die Eckpunkte des ASAR-Bildes, die von der Arbeitsgruppe 0 in geographischen Koordinaten übergeben wurden, werden ebenfalls in polarstereographische Koordinaten umgerechnet
- Die Koordinatentransformation wird so durchgeführt, dass man als Ergebnis den ICESat-Datensatz als normierte Bildkoordinaten erhält. Dazu werden zunächst die vier ASAR-Eckpunkte in normierte Bildkoordinaten gebracht und anschließend die ICESat-Daten auf dasselbe Koordiantensystem transformiert.

- Als Endergebnis wird eine Matrix erzeugt, die die Messpositionen des ICESat-Ueberfluges im ASAR-Auschnitt in Bildkoordinaten und die zugeoerigen Freibordoehen enthält.
Ergebnisse
Der Output besteht dann wie oben gesagt aus einer Matrix mit den Messpositionen des ICESat-Ueberfluges und der zugehoerigen Freibordhoehen.
(Output, Statistik)
Diskussion
Programme
fbh_bildkoordinaten.py
1 from polar_projection import *
2 from read_asar import *
3 from read_icesat import *
4 from coord_transform import *
5 from scipy import *
6
7 def fit_freeboard_ASAR(filename1,filename2):
8 """filename1: ASAR data file, filename2: freeboard data file
9 creates new coordinate system defined by corners of ASAR image and selects freeboard values within ASAR image box
10 returns an array containing normalized image coordinates and corresponding freeboard values:
11 [x_coordinate, y_coordinate, freeboardheight(cm)]"""
12
13 sgn=-1 #Antarctica
14 ASAR=array(read_asar_corners(filename1))
15 ASAR_p=zeros(8)
16 for k in arange(0,7,2): #computing polarstereographic coordinates
17 ASAR_p[k:k+2]=mapll(ASAR[k],ASAR[k+1],sgn)
18
19 A=coord_transformation(ASAR_p) #computing transformation matrix A for coordinate
20 #transformation into image coordinates
21
22 # reading freeboard data and computing geographic into polarstereographic coordinates
23 ICESAT_p,fbh=read_icesat(filename2,sgn) #fbh are measured freeboard heights in cm
24
25 # calculating new coordinates for freeboard data
26 x_neu=[]
27 y_neu=[]
28 for x,y in zip(ICESAT_p[0],ICESAT_p[1]):
29 x_neu.append(dot(array([A[0,0],A[0,1]]),array([x,y]))+A[0,2])
30 y_neu.append(dot(array([A[1,0],A[1,1]]),array([x,y]))+A[1,2])
31 x_n=array(x_neu)
32 y_n=array(y_neu)
33 fbh_n=array(fbh)
34
35 x_n_limited=clip(x_n,0.,1.)
36 x_indices=nonzero(x_n==x_n_limited)
37 x_xind=x_n[x_indices]
38 y_xind=y_n[x_indices]
39 fbh_xind=fbh_n[x_indices]
40
41 y_n_limited=clip(y_xind,0.,1.)
42 y_indices=nonzero(y_xind==y_n_limited)
43 x_bild=x_xind[y_indices]
44 y_bild=y_xind[y_indices]
45 fbh_bild=fbh_xind[y_indices]
46
47 x_y_fbh=array([x_bild,y_bild,fbh_bild])
48
49 return x_y_fbh
coord_transform.py
1 from scipy import linalg as la
2
3 def coord_transformation(ASAR_p):
4 # polarstereographic coordinate system
5 y00,x00,y01,x01,y02,x02,y03,x03=int(ASAR_p[1]),int(ASAR_p[0]),int(ASAR_p[7]),int(ASAR_p[6]),int(ASAR_p[5]),int(ASAR_p[4]),int(ASAR_p[3]),int(ASAR_p[2])
6 # new coordinate system with normalized coordinates
7 y10,x10,y11,x11,y12,x12,y13,x13=0,0,1,0,1,1,0,1
8
9 # calculating transformation matrix:
10 P0=array([[x00, x01, x02, x03],[y00,y01,y02,y03],[1.0,1.0,1.0,1.0]])
11 P1=array([[x10, x11, x12, x13],[y10,y11,y12,y13],[1.0,1.0,1.0,1.0]])
12
13 Faktor1=dot(P1,la.transpose(P0))
14 Faktor2=la.inverse(dot(P0,la.transpose(P0)))
15 A=dot(Faktor1,Faktor2) # Transformation matrix
16 return A
read_icesat.py
Die benötigten Module polar_projection.py und read_asar.py sind auf der Seite der Arbeitsgruppe 0 AG0_ASAR_Einlesen zu finden.
fbh_bildkoordinaten_test.py
Zum Testen hängt man an das obige Programm folgende Zeilen an: