|
Size: 6629
Comment:
|
← Revision 29 as of 2008-07-11 11:19:34 ⇥
Size: 6770
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| Die Besprechung ueber das Vorgehen ihrer Aufgaben ergab: | === Arbeitsgruppe 1: Freibord === Die Aufgabe der Arbeitsgruppe bestand darin, die I |
| Line 3: | Line 5: |
| die Transformation in polarstereographische Koordinaten und der nachfolgende Uebergang zu den Bildpunkten von ASAR Eckpunkte und Aufloseung des ASAR-Bildes variieren frei -> allgemeingueltiges Programm fuer den Uebergang der Output erfolgt als Vektor in der Form x, y, Freiboardhoehe; eventuell die Floatangabe |
'''Daten''' Der Gruppe stand ein ASAR-Satellitenbild zur Verfügung, das einen Auschnitt des Weddellmeeres zeigt und ein ICESat-Datensatz, der die geographischen Positionen (lon, lat) und die an diesen Punkten gemessenen Freibordhöhen (cm) für einen Überflug quer durch den ASAR-Ausschnitt beinhaltet. {{attachment:schema1.jpg}} '''Methodik''' Theorie zur Koordinatentransformation: Eine affine Abbildung ist eine lineare Koordinatentransformation, die die elementaren Transformationen Translation, Rotation, Dilatation, Stauchung und Scherung umfasst. Sie kann durch Vektoraddition und Matrixmultiplikation ausgedrueckt werden: {{{#!latex \[\left(\begin{array}{c} x' \\ y' \end{array}\right) = \left(\begin{array}[c]{ccc} a_{\rm{11}} & a_{\rm{12}}\\a_{\rm{21}} & a_{\rm{22}}\end{array}\right) \left(\begin{array}{c} x \\ y \end{array}\right) + \left(\begin{array}{c} t_x \\ t_y \end{array}\right)\] }}} Homogene Koordinaten: {{{#!latex \[\left(\begin{array}{c} x' \\ y' \\ 1 \end{array}\right) = \left(\begin{array}[c]{ccc} a_{\rm{11}} & a_{\rm{12}} & t_x \\ a_{\rm{21}} & a_{\rm{22}} & t_y \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{c} x \\ y \\ 1 \end{array}\right)\] }}} Für drei nichtkollineare Punkte ergibt sich damit folgendes Gleichungssystem: {{{#!latex \[\left(\begin{array}[c]{ccc} x_1' & x_2' & x_3' \\ y_1' & y_2' & y_3' \\ 1 & 1 & 1 \end{array}\right)= \left(\begin{array}[c]{ccc} a_{\rm{11}} & a_{\rm{12}} & t_x \\ a_{\rm{21}} & a_{\rm{22}} & t_y \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}[c]{ccc} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 & 1 \end{array}\right)\] }}} oder {{{#!latex \[P'=AP\] }}} Die Transformationsmatrix A für drei nichtkollineare Punkte lässt sich dann einfach aus {{{#!latex \[A=P'P^{-1}\] }}} bestimmen. Transformationskoeffizienten für mehr als drei nichtkollineare Punkte erhält man mit der Methode der kleinsten Quadrate aus: {{{#!latex \[A=P'P^T(PP^T)^{-1}\] }}} (für mehr Informationen siehe B. Jähne, Digitale Bildverarbeitung, Kapitel 10.4) |
| Line 8: | Line 54: |
| Arbeitsschritte: Die Gruppe hat Programme bzw. Funktionen erarbeitet, die folgendes tun: * Einlesen der ICESat-Datei und umrechnen der geographischen Koordinaten des Ueberfluges in polarstereographische Koordinaten. * Die Eckpunkte des ASAR-Bildes, die von der Arbeitsgruppe 0 in geographischen Koordinaten übergeben wurden, werden ebenfalls in polarstereographische Koordinaten umgerechnet * Die Koordinatentransformation wird so durchgeführt, dass man als Ergebnis den ICESat-Datensatz als normierte Bildkoordinaten erhält. Dazu werden zunächst die vier ASAR-Eckpunkte in normierte Bildkoordinaten gebracht und anschließend die ICESat-Daten auf dasselbe Koordiantensystem transformiert. {{attachment:schema.jpg}} * Als Endergebnis wird eine Matrix erzeugt, die die Messpositionen des ICESat-Ueberfluges im ASAR-Auschnitt in Bildkoordinaten und die zugeoerigen Freibordoehen enthält. '''Ergebnisse''' Der Output besteht dann wie oben gesagt aus einer Matrix mit den Messpositionen des ICESat-Ueberfluges und der zugehoerigen Freibordhoehen. (Output, Statistik) '''Diskussion''' === Programme === |
|
| Line 14: | Line 80: |
| import string | from read_icesat import * from coord_transform import * from scipy import * |
| Line 16: | Line 84: |
| def fit_freeboard_ASAR(filename1,filename2,resolution): """filename1: ASAR data file, filename2: freeboard data file, resolution: ASAR image data resolution creates new coordinate system defined by corners of ASAR image and selects freeboard values within ASAR image box and returns an array containing normalized image coordinates and corresponding freeboard values: |
def fit_freeboard_ASAR(filename1,filename2): """filename1: ASAR data file, filename2: freeboard data file creates new coordinate system defined by corners of ASAR image and selects freeboard values within ASAR image box returns an array containing normalized image coordinates and corresponding freeboard values: |
| Line 24: | Line 91: |
| lat1,lon1,lat2,lon2,lat3,lon3,lat4,lon4=read_asar_corners(filename1) | ASAR=array(read_asar_corners(filename1)) ASAR_p=zeros(8) for k in arange(0,7,2): #computing polarstereographic coordinates ASAR_p[k:k+2]=mapll(ASAR[k],ASAR[k+1],sgn) A=coord_transformation(ASAR_p) #computing transformation matrix A for coordinate #transformation into image coordinates # reading freeboard data and computing geographic into polarstereographic coordinates ICESAT_p,fbh=read_icesat(filename2,sgn) #fbh are measured freeboard heights in cm # calculating new coordinates for freeboard data x_neu=[] y_neu=[] for x,y in zip(ICESAT_p[0],ICESAT_p[1]): x_neu.append(dot(array([A[0,0],A[0,1]]),array([x,y]))+A[0,2]) y_neu.append(dot(array([A[1,0],A[1,1]]),array([x,y]))+A[1,2]) x_n=array(x_neu) y_n=array(y_neu) fbh_n=array(fbh) x_n_limited=clip(x_n,0.,1.) x_indices=nonzero(x_n==x_n_limited) x_xind=x_n[x_indices] y_xind=y_n[x_indices] fbh_xind=fbh_n[x_indices] |
| Line 26: | Line 118: |
| ASAR_1=[lat1,lon1] ASAR_2=[lat2,lon2] ASAR_3=[lat3,lon3] ASAR_4=[lat4,lon4] |
y_n_limited=clip(y_xind,0.,1.) y_indices=nonzero(y_xind==y_n_limited) x_bild=x_xind[y_indices] y_bild=y_xind[y_indices] fbh_bild=fbh_xind[y_indices] x_y_fbh=array([x_bild,y_bild,fbh_bild]) |
| Line 31: | Line 126: |
| ASAR_1p=mapll(ASAR_1[0],ASAR_1[1],sgn) #computing polarstereographic coordinates ASAR_2p=mapll(ASAR_2[0],ASAR_2[1],sgn) ASAR_3p=mapll(ASAR_3[0],ASAR_3[1],sgn) ASAR_4p=mapll(ASAR_4[0],ASAR_4[1],sgn) |
return x_y_fbh }}} |
| Line 36: | Line 129: |
| X=int(abs(ASAR_2p[0]-ASAR_1p[0])/resolution) #image size in pixel Y=int(abs(ASAR_4p[1]-ASAR_1p[1])/resolution) |
'''coord_transform.py''' {{{#!python from scipy import linalg as la |
| Line 39: | Line 133: |
| def coord_transformation(ASAR_p): | |
| Line 40: | Line 135: |
| y00,x00,y01,x01,y02,x02,y03,x03=int(ASAR_1p[1]),int(ASAR_1p[0]),int(ASAR_4p[1]),int(ASAR_4p[0]),int(ASAR_3p[1]),int(ASAR_3p[0]),int(ASAR_2p[1]),int(ASAR_2p[0]) | y00,x00,y01,x01,y02,x02,y03,x03=int(ASAR_p[1]),int(ASAR_p[0]),int(ASAR_p[7]),int(ASAR_p[6]),int(ASAR_p[5]),int(ASAR_p[4]),int(ASAR_p[3]),int(ASAR_p[2]) |
| Line 48: | Line 143: |
| Faktor1=dot(P1,transpose(P0)) Faktor2=inverse(dot(P0,transpose(P0))) A=dot(Faktor1,Faktor2) # Transformation matrix |
Faktor1=dot(P1,la.transpose(P0)) Faktor2=la.inverse(dot(P0,la.transpose(P0))) A=dot(Faktor1,Faktor2) # Transformation matrix return A }}} |
| Line 52: | Line 149: |
| # reading freeboard data lon=[] lat=[] fbh=[] datei = open (filename2, 'r') line=datei.readline() k=-1 while line!="": k=k+1 data=string.split(line) lon.append(float(data[0])) lat.append(abs(float(data[1]))) fbh.append(float(data[2])) line=datei.readline() |
'''read_icesat.py''' |
| Line 67: | Line 151: |
| polar=mapll(array(lat),array(lon),sgn) | {{{#!python # reading freeboard data |
| Line 69: | Line 154: |
| # calculating new coordinates for freeboard data x_neu=[] y_neu=[] for x,y in zip(polar[0],polar[1]): x_neu.append(dot(array([A[0,0],A[0,1]]),array([x,y]))+A[0,2]) y_neu.append(dot(array([A[1,0],A[1,1]]),array([x,y]))+A[1,2]) |
import string from geo_polar import * from scipy import io |
| Line 76: | Line 158: |
| # cutting off non-corresponding data values m=-1 index_vec=[] for xn,yn in zip(x_neu,y_neu): m=m+1 if xn<=1. and xn >=0. and yn<=1. and yn >=0.: index_vec.append(m) x_bild=[] y_bild=[] fbh_bild=[] for i in index_vec: x_bild.append(x_neu[i]) y_bild.append(y_neu[i]) fbh_bild.append(fbh[i]) x_y_fbh=array([x_bild,y_bild,fbh_bild]) return x_y_fbh |
def read_icesat(filename,sgn): data=io.read_array(filename) polar=mapll(data[:,1],data[:,0],sgn) fbh=data[:,2] return polar,fbh |
| Line 102: | Line 169: |
| Zum Testen hängt man an das obige Programm folgende Zeilen an: | |
| Line 103: | Line 171: |
| from polar_projection import * from read_asar import * import string def fit_freeboard_ASAR(filename1,filename2,resolution): """filename1: ASAR data file, filename2: freeboard data file, resolution: ASAR image data resolution creates new coordinate system defined by corners of ASAR image and selects freeboard values within ASAR image box returns an array containing normalized image coordinates and corresponding freeboard values: [x_coordinate, y_coordinate, freeboardheight(cm)]""" sgn=-1 #Antarctica lat1,lon1,lat2,lon2,lat3,lon3,lat4,lon4=read_asar_corners(filename1) ASAR_1=[lat1,lon1] ASAR_2=[lat2,lon2] ASAR_3=[lat3,lon3] ASAR_4=[lat4,lon4] ASAR_1p=mapll(ASAR_1[0],ASAR_1[1],sgn) #computing polarstereographic coordinates ASAR_2p=mapll(ASAR_2[0],ASAR_2[1],sgn) ASAR_3p=mapll(ASAR_3[0],ASAR_3[1],sgn) ASAR_4p=mapll(ASAR_4[0],ASAR_4[1],sgn) X=int(abs(ASAR_2p[0]-ASAR_1p[0])/resolution) #image size in pixel Y=int(abs(ASAR_4p[1]-ASAR_1p[1])/resolution) # polarstereographic coordinate system y00,x00,y01,x01,y02,x02,y03,x03=int(ASAR_1p[1]),int(ASAR_1p[0]),int(ASAR_4p[1]),int(ASAR_4p[0]),int(ASAR_3p[1]),int(ASAR_3p[0]),int(ASAR_2p[1]),int(ASAR_2p[0]) # new coordinate system with normalized coordinates y10,x10,y11,x11,y12,x12,y13,x13=0,0,1,0,1,1,0,1 # calculating transformation matrix: P0=array([[x00, x01, x02, x03],[y00,y01,y02,y03],[1.0,1.0,1.0,1.0]]) P1=array([[x10, x11, x12, x13],[y10,y11,y12,y13],[1.0,1.0,1.0,1.0]]) Faktor1=dot(P1,transpose(P0)) Faktor2=inverse(dot(P0,transpose(P0))) A=dot(Faktor1,Faktor2) # Transformation matrix # reading freeboard data lon=[] lat=[] fbh=[] datei = open (filename2, 'r') line=datei.readline() k=-1 while line!="": k=k+1 data=string.split(line) lon.append(float(data[0])) lat.append(abs(float(data[1]))) fbh.append(float(data[2])) line=datei.readline() polar=mapll(array(lat),array(lon),sgn) # calculating new coordinates for freeboard data x_neu=[] y_neu=[] for x,y in zip(polar[0],polar[1]): x_neu.append(dot(array([A[0,0],A[0,1]]),array([x,y]))+A[0,2]) y_neu.append(dot(array([A[1,0],A[1,1]]),array([x,y]))+A[1,2]) # cutting off non-corresponding data values m=-1 index_vec=[] for xn,yn in zip(x_neu,y_neu): m=m+1 if xn<=1. and xn >=0. and yn<=1. and yn >=0.: index_vec.append(m) x_bild=[] y_bild=[] fbh_bild=[] for i in index_vec: x_bild.append(x_neu[i]) y_bild.append(y_neu[i]) fbh_bild.append(fbh[i]) x_y_fbh=array([x_bild,y_bild,fbh_bild]) return x_y_fbh |
|
| Line 189: | Line 173: |
| resolution=0.025 ergebnis=fit_freeboard_ASAR(filename1,filename2,resolution) |
ergebnis=fit_freeboard_ASAR(filename1,filename2) |
| Line 193: | Line 176: |
| {{attachment:schemabild.eps}} | {{attachment.schemabild2.jpg}} |
Arbeitsgruppe 1: Freibord
Die Aufgabe der Arbeitsgruppe bestand darin, die I
Daten
Der Gruppe stand ein ASAR-Satellitenbild zur Verfügung, das einen Auschnitt des Weddellmeeres zeigt und ein ICESat-Datensatz, der die geographischen Positionen (lon, lat) und die an diesen Punkten gemessenen Freibordhöhen (cm) für einen Überflug quer durch den ASAR-Ausschnitt beinhaltet.
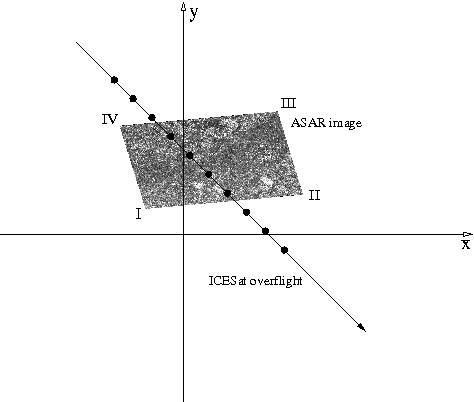
Methodik
Theorie zur Koordinatentransformation:
Eine affine Abbildung ist eine lineare Koordinatentransformation, die die elementaren Transformationen Translation, Rotation, Dilatation, Stauchung und Scherung umfasst. Sie kann durch Vektoraddition und Matrixmultiplikation ausgedrueckt werden:
latex error! exitcode was 2 (signal 0), transscript follows:
Homogene Koordinaten:
latex error! exitcode was 2 (signal 0), transscript follows:
Für drei nichtkollineare Punkte ergibt sich damit folgendes Gleichungssystem:
latex error! exitcode was 2 (signal 0), transscript follows:
oder
latex error! exitcode was 2 (signal 0), transscript follows:
Die Transformationsmatrix A für drei nichtkollineare Punkte lässt sich dann einfach aus
latex error! exitcode was 2 (signal 0), transscript follows:
bestimmen.
Transformationskoeffizienten für mehr als drei nichtkollineare Punkte erhält man mit der Methode der kleinsten Quadrate aus:
latex error! exitcode was 2 (signal 0), transscript follows:
(für mehr Informationen siehe B. Jähne, Digitale Bildverarbeitung, Kapitel 10.4)
Arbeitsschritte:
Die Gruppe hat Programme bzw. Funktionen erarbeitet, die folgendes tun:
- Einlesen der ICESat-Datei und umrechnen der geographischen Koordinaten des Ueberfluges in polarstereographische Koordinaten.
- Die Eckpunkte des ASAR-Bildes, die von der Arbeitsgruppe 0 in geographischen Koordinaten übergeben wurden, werden ebenfalls in polarstereographische Koordinaten umgerechnet
- Die Koordinatentransformation wird so durchgeführt, dass man als Ergebnis den ICESat-Datensatz als normierte Bildkoordinaten erhält. Dazu werden zunächst die vier ASAR-Eckpunkte in normierte Bildkoordinaten gebracht und anschließend die ICESat-Daten auf dasselbe Koordiantensystem transformiert.

- Als Endergebnis wird eine Matrix erzeugt, die die Messpositionen des ICESat-Ueberfluges im ASAR-Auschnitt in Bildkoordinaten und die zugeoerigen Freibordoehen enthält.
Ergebnisse
Der Output besteht dann wie oben gesagt aus einer Matrix mit den Messpositionen des ICESat-Ueberfluges und der zugehoerigen Freibordhoehen.
(Output, Statistik)
Diskussion
Programme
fbh_bildkoordinaten.py
1 from polar_projection import *
2 from read_asar import *
3 from read_icesat import *
4 from coord_transform import *
5 from scipy import *
6
7 def fit_freeboard_ASAR(filename1,filename2):
8 """filename1: ASAR data file, filename2: freeboard data file
9 creates new coordinate system defined by corners of ASAR image and selects freeboard values within ASAR image box
10 returns an array containing normalized image coordinates and corresponding freeboard values:
11 [x_coordinate, y_coordinate, freeboardheight(cm)]"""
12
13 sgn=-1 #Antarctica
14 ASAR=array(read_asar_corners(filename1))
15 ASAR_p=zeros(8)
16 for k in arange(0,7,2): #computing polarstereographic coordinates
17 ASAR_p[k:k+2]=mapll(ASAR[k],ASAR[k+1],sgn)
18
19 A=coord_transformation(ASAR_p) #computing transformation matrix A for coordinate
20 #transformation into image coordinates
21
22 # reading freeboard data and computing geographic into polarstereographic coordinates
23 ICESAT_p,fbh=read_icesat(filename2,sgn) #fbh are measured freeboard heights in cm
24
25 # calculating new coordinates for freeboard data
26 x_neu=[]
27 y_neu=[]
28 for x,y in zip(ICESAT_p[0],ICESAT_p[1]):
29 x_neu.append(dot(array([A[0,0],A[0,1]]),array([x,y]))+A[0,2])
30 y_neu.append(dot(array([A[1,0],A[1,1]]),array([x,y]))+A[1,2])
31 x_n=array(x_neu)
32 y_n=array(y_neu)
33 fbh_n=array(fbh)
34
35 x_n_limited=clip(x_n,0.,1.)
36 x_indices=nonzero(x_n==x_n_limited)
37 x_xind=x_n[x_indices]
38 y_xind=y_n[x_indices]
39 fbh_xind=fbh_n[x_indices]
40
41 y_n_limited=clip(y_xind,0.,1.)
42 y_indices=nonzero(y_xind==y_n_limited)
43 x_bild=x_xind[y_indices]
44 y_bild=y_xind[y_indices]
45 fbh_bild=fbh_xind[y_indices]
46
47 x_y_fbh=array([x_bild,y_bild,fbh_bild])
48
49 return x_y_fbh
coord_transform.py
1 from scipy import linalg as la
2
3 def coord_transformation(ASAR_p):
4 # polarstereographic coordinate system
5 y00,x00,y01,x01,y02,x02,y03,x03=int(ASAR_p[1]),int(ASAR_p[0]),int(ASAR_p[7]),int(ASAR_p[6]),int(ASAR_p[5]),int(ASAR_p[4]),int(ASAR_p[3]),int(ASAR_p[2])
6 # new coordinate system with normalized coordinates
7 y10,x10,y11,x11,y12,x12,y13,x13=0,0,1,0,1,1,0,1
8
9 # calculating transformation matrix:
10 P0=array([[x00, x01, x02, x03],[y00,y01,y02,y03],[1.0,1.0,1.0,1.0]])
11 P1=array([[x10, x11, x12, x13],[y10,y11,y12,y13],[1.0,1.0,1.0,1.0]])
12
13 Faktor1=dot(P1,la.transpose(P0))
14 Faktor2=la.inverse(dot(P0,la.transpose(P0)))
15 A=dot(Faktor1,Faktor2) # Transformation matrix
16 return A
read_icesat.py
Die benötigten Module polar_projection.py und read_asar.py sind auf der Seite der Arbeitsgruppe 0 AG0_ASAR_Einlesen zu finden.
fbh_bildkoordinaten_test.py
Zum Testen hängt man an das obige Programm folgende Zeilen an:
